I – Introduction
Voir activité.
II – Fonction réciproque
Définition
Soit f une fonction continue strictement monotone sur un intervalle I=[a;b].
Il existe une fonction définie sur J=[f(a);f(b)] (ou [f(b);f(a)]) et à valeurs dans I, appelée fonction réciproque de f et notée f^{-1} telle que:
\left\{ \begin{array}{c c} x &=& f^{-1}(y)\\ y &\in& J \end{array} \right. \Leftrightarrow \left\{ \begin{array}{c c} y &=& f(x)\\ x &\in& I \end{array} \right.
Dans un repère orthonormé, les courbes représentatives des fonctions f et f^{-1} sontsymétriques par rapport à la droite d’équation y=x.
Exemple
- La fonction carrée est continue strictement croissante sur ]0;+\infty[ à valeurs dans ]0;+\infty[. Donc la fonction carrée admet donc une fonction réciproque sur ]0;+\infty[: c’est la fonction racine carrée, définie sur ]0;+\infty[ et à valeurs dans ]0;+\infty[.
Si on trace les courbes représentatives de ces deux fonctions dans le même repère orthonormé, elles sont bien symétriques par rapport à la droite d’équation y=x.
Propriété
Soit f une fonction définie, continue et strictement monotone sur un intervalle I et à valeurs dans un intervalle J, de fonction réciproque f^{-1}.
\forall x\in J, f\left(f^{-1}(x)\right)=x
\forall x\in I, f^{-1}\left(f(x)\right)=x
Exemple
La fonction racine carrée est la fonction réciproque de la fonction carrée donc:
\forall x\in ]0;+\infty[, \left(\sqrt{x}\right)^2=x
\forall x\in ]0;+\infty[, \sqrt{x^2}=x
III – Fonction logarithme néperien
La fonction exponentielle est continue strictement croissante sur \mathbb{R} à valeurs dans ]0;+\infty[ donc il existe une fonction réciproque à la fonction exponentielle. Elle s’appelle fonction logarithme néperien. Elle est définie sur ]0;+\infty[ et à valeur dans \mathbb{R}.
Définition
La fonction logarithme néperien, notée ln est la fonction réciproque de la fonction exponentielle.
Elle est définie sur ]0;+\infty[.
Propriété
ln(1)=0
ln(e)=1
Démonstration
La fonction ln est la fonction réciproque de la fonction exponentielle.
Or e^0=1 donc 0=ln(1)
De plus e^1=e donc 1=ln(e)
Courbe représentative
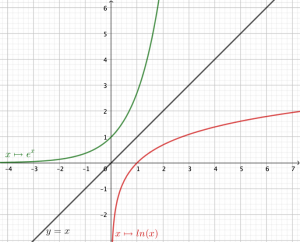
Les courbes représentatives des fonctions logarithme néperien et exponentielle sont symétriques par rapport à la droite d’équation y=x.
Propriété
- \forall y \in ]0:+\infty[, \forall x \in \mathbb{R}, e^x=y\Leftrightarrow x=ln(y)
- \forall x\in ]0;+\infty[, e^{ln(x)}=x
- \forall x\in \mathbb{R}, ln\left(e^x\right)=x
Propriété
Soient a et b deux nombres réels strictement positifs. On a:
- ln(ab)=ln(a)+ln(b)
- ln\left(\frac{1}{b}\right)=-ln(b)
- ln\left(\frac{a}{b}\right)=ln(a)-ln(b)
- \forall n\in \mathbb{N}, ln\left(a^n\right)=nln(a)
- ln\left(\sqrt{a}\right)=\frac{1}{2}ln(a)
Démonstration
- Posons A=ln(ab) et B=ln(a)+ln(b).
A=ln(ab) \Leftrightarrow e^A=ab\\B=ln(a)+ln(b)\Leftrightarrow e^B=e^{ln(a)+ln(b)}=e^{ln(a)}e^{ln(b)}=abDonc e^A=e^B
Donc A=ln(e^A)=ln(e^B)=B
Ainsi ln(ab)=ln(a)+ln(b)
- ln(b)+ln\left(\frac{1}{b}\right)=ln\left(b\times \frac{1}{b}\right)=ln(1)=0 donc ln\left(\frac{1}{b}\right)=-ln(b)
- ln\left(\frac{a}{b}\right)+ln(b)=ln\left(\frac{a}{b}\times b\right)=ln(a) donc ln\left(\frac{a}{b}\right)=ln(a)-ln(b)
- Posons A=ln\left(a^n\right) et B=nln(a)\\ A=ln\left(a^n\right)\Leftrightarrow e^A=a^n\\ B=nln(a) \Leftrightarrow e^B=e^{nln(a)}=\left(e^{ln(a)}\right)^n=a^n
Donc e^A=e^B\\
Donc A=ln(e^A)=ln(e^B)=B\\
Ainsi ln\left(a^n\right)=nln(a).- 2ln\left(\sqrt{a}\right)=ln\left(\sqrt{a}^2\right)=ln(a)
Donc ln\left(\sqrt{a}\right)=\frac{1}{2}ln(a)
IV – Etude de la fonction logarithme néperien
Propriété
La fonction ln est dérivable sur l’intervalle ]0;+\infty[ et \forall x\in ]0;+\infty[, ln'(x)=\frac{1}{x}.
Démonstration
On admet la dérivabilité de la fonction ln sur ]0;+\infty[.
On sait que \forall x\in ]0;+\infty[, e^{ln(x)}=x.
Donc on a:
ln'(x)e^{ln(x)}=1
Soit encore ln'(x)\times x=1
Ainsi ln'(x)=\frac{1}{x}.
Propriété
\lim \limits_{x\mapsto +\infty} ln(x)=+\infty
\lim \limits_{x\mapsto 0\\ x>0} ln(x)=-\infty
Variations de la fonction ln
La fonction ln est strictement croissante sur ]0;+\infty[.
Démonstration
\forall x\in ]0;+\infty[, ln'(x)=\frac{1}{x}
Donc \forall x\in ]0;+\infty[, ln'(x)>0
Ainsi la fonction ln est strictement croissante sur ]0;+\infty[.
Propriété
Soit u une fonction dérivable et strictement positive sur un intervalle I.
La fonction f:x\mapsto ln(u(x)) est dérivable sur I et f'(x)=\frac{u'(x)}{u(x)}.
Démonstration
Soit a \in I.
\frac{f(a+h)-f(a)}{h}=\frac{ln(u(a+h))-ln(u(a))}{h}=\frac{ln(u(a+h))-ln(u(a))}{u(a+h)-u(a)}\times \frac{u(a+h)-u(a)}{h}
Nous allons calculer \lim \limits_{h\mapsto 0}\frac{f(a+h)-f(a)}{h}.D’une part, \lim \limits_{h\mapsto 0} \frac{u(a+h)-u(a)}{h}=u'(a)
D’autre part, \lim \limits_{h\mapsto 0}u(a+h)-u(a)=0
Posons H=u(a+h)-u(a)
\frac{ln(u(a+h))-ln(u(a))}{u(a+h)-u(a)}=\frac{ln(u(a+h)-u(a)+u(a))-ln(u(a))}{H}=\frac{ln(H+u(a))-ln(u(a))}{H}
Or \lim \limits_{h\mapsto 0}H=0
Donc \lim \limits_{h\mapsto 0}\frac{ln(u(a)+H)-ln(u(a))}{H}=ln'(u(a))=\frac{1}{u(a)}
Ainsi \lim \limits_{h\mapsto 0}\frac{f(a+h)-f(a)}{h}=\lim \limits_{h\mapsto 0}\frac{ln(u(a+h))-ln(u(a))}{u(a+h)-u(a)}\times \frac{u(a+h)-u(a)}{h}=\frac{1}{u(a)}\times u'(a)=\frac{u'(a)}{u(a)}
\forall a \in I, \lim \limits_{h\mapsto 0}\frac{f(a+h)-f(a)}{h}=\frac{u'(a)}{u(a)}
Exemple
Déterminer la fonction dérivée de la fonction f:x\mapsto ln(x^2-1) définie sur ]1;+\infty[.
Posons u(x)=x^2-1
u est dérivable sur ]1;+\infty[ et u'(x)=2x.
De plus, on a bien u(x)>0 sur ]1;+\infty[.
Donc f'(x)=\frac{2x}{x^2-1}
V – Quelques problèmes
1. Déterminer un seuil
On estime que la concentration de to xines dans le sang des poissons d’un lac
augmente de 5 % par an.
Elle est actuellement en moyenne de 2 ppm (part ie par millions).
L’algorithme ci-dessous détermine le nombre d’années au bout duquel la concentration dépassera une valeur C (C\ge 2) donnée.
Tant que u < C
u\leftarrow 1,05\times u
n\leftarrow n+1
Fin Tant que
Au début de l’algorithme, on affecte 0 à la variable n et 2 à la variable u.
- Exécuter l’algorithme pas à pas, en complétant un tableau de suivi des variables, lorsque C = 2,4. Arrondir au centième si besoin.
- Coder cet algorithme à l’aide d’une fonction
seuil[/katex] de paramètre C écrite en langage Python.
Saisir et exécuter ce programme pour C = 3,5. Interpréter dans le contexte de la situation. - Retrouver le résultat du b) par le calcul.
2. Algorithme de Briggs
On souhaite déterminer une approximation du nombre ln(2) à l'aide d'un algorithme publié en 1617 par Henri Briggs.
- a. Recopier et compléter le tableau de valeurs ci-dessous. Arrondir au dix -millième si besoin.
x 0,999 0,9995 1 1,0005 1,001 ln(x) x-1 b. Que constate-t-on?
On admet que si x\in[0,999;1,001] alors ln(x)\approx x-1. - Soit \left(u_n\right)_{n\in\mathbb{N}} la suite définie par u_0=2 et \forall n\in\mathbb{N},u_{n+1}=\sqrt{u_n}.
a. Justifier que ln(u_1)=\frac{1}{2}ln(2), ln(u_2)=\left(\frac{1}{2}\right)^2ln(2) et ln(u_3)=\left(\frac{1}{2}\right)^3ln(2).
b. On admet que \forall n\in\mathbb{N}, ln(u_n)=\left(\frac{1}{2}\right)^nln(2).
Expliquer pourquoi si 0,999\le u_n\le 1,001, alors ln(2)\approx(u_n-1°2^n. - Voici un programme écrit en langage Python.
from math import sqrt def approx(): u = 2 n = 0 while u > 1.001: u = sqrt(u) n = n+1 l = (u-1)*2**n l = round(l,3) return l[/katex]a. Saisir, puis exécuter la fonctionapprox[/katex].
b. Donner, à l'aide de la calculatrice, une valeur approchée à 10^{-3} près de ln(2).
c. Quel est le rôle de ce programme ?
3. Modèle issu de contextes physique: optimisation
Lors d'une expérience en laboratoire, on lance un projectile dans un milieu fluide. Le projectile ne se déplaçant pas dans l'air mais dans un fluide, le modèle parabolique usuel n'est pas adapté.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction f définie sur l'intervalle [ 0; 1[ par :
f(x)=bx+2 ln(1- x)
où b est un paramètre réel supérieur ou égal à 2, x est l'abscisse du projectile, f(x) son ordonnée, toutes les deux exprimées en mètre.
Nous allons déterminer pour quel angle de tir \theta, par rapport à l'horizontale, la hauteur du projectile ne dépasse pas 1,6~m.
Partie A: déterminer la hauteur du projectile
- Dans cette question, on choisit b = 5.
a. Vérifier que pour tout réel x de l'intervalle [0; 1[, f'(x) =\frac{3-5x}{1-x}
b. Étudier les variations de f sur l'intervalle [0; 1[.
c. En déduire la hauteur maximum atteinte par le projectile. Donner la valeur exacte, puis l'arrondi au centième. - Dans cette question on çhoisit b = 6.
Déterminer , comme dans la question précédente, la hauteur maximum atteinte
par le projectile. Arrondir au centième. - On choisit à présent une valeur quelconque de b dans l'intervalle [2; +\infty[.
a. Justifier que pour tout réel x de l'intervalle [0; 1[, f '(x) = \frac{-bx+b-2}{1-x}.
b. Démontrer que pour tout réel b \ge 2, 0\le \frac{b-2}{b}\le 1.
c. Justifier que f possède un maximum sur l'intervalle [0;1[ égal à `$$b - 2+ 2ln\left(\frac{2}{b}\right)$
Partie B: déterminer l'angle de tir
- g est la fonction définie sur l'intervalle [2; +\infty[ par g(x) = x- 2 + 2 ln\left(\frac{2}{x}\right).
a. Justifier que pour tout réel x de l'intervalle [2; +\infty[, g'(x) = \frac{x-2}{x}.
b. En déduire le tableau de variations de la fonction g.
On admet que \lim \limits_{x\mapsto +\infty} g(x) = +\infty. - a. Démontrer que l'équation g(x) = 1,6 admet une unique solution a dans l'intervalle [2 ; +\infty[.
b. Compléter le programme ci-dessous écrit en langage Python, afin que la fonctionsolution[/katex] renvoie la valeur approchée au centième par défaut de a.from math import log def g(x): y=x-2+2*log(2/x) return y def solution(): x=2 a=g(x) while a< ... : x=x+0.01 a= ... x=round(x-0.01,2) return x[/katex]c. Saisir et exécuter ce programme. Préciser la valeur approchée de a obtenue.
Interpréter concrètement ce résultat. - Dans cette question, on choisit b = 5,69.
On a représenté ci-dessous la courbe de la fonction f.

L'angle de tir \theta correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction f au point d'abscisse comme indiqué sur le schéma donné ci-dessus.
Déterminer l'angle \theta. Arrondir au dixième.
4. Travaux de Neper
Au 17e siècle, Neper bâtit sa conception du logarithme par des procédés cinématiques. Il imagine deux points mobiles se déplaçant sur deux axes parallèles, l'un se déplaçant à une vitesse constante et l'autre se déplaçant à une vitesse proportionnelle à la distance lui restant à parcourir.
Il parvient ainsi à établir l'encadrement suivant du logarithme:
\forall x\in ]0;+\infty[, \frac{x-1}{x}\le ln(x)\le x-1
Nous allons démontrer cet encadrement et l'utiliser.
Partie A: une démonstration de l'encadrement utilisé par Neper
f et g sont les fonctions définies sur l'intervalle ]0;+\infty [ par:
f(x)=ln(x)-x+1
g(x)=ln(x)-\frac{x-1}{x}
- a. Vérifier que pour tout réel x > 0, f'(x)=\frac{1-x}{x}.
b. Etudier le sens de variation de la fonction f.
c. En déduire que pour tout réel x > 0, ln(x)\le x-1. - a. Vérifier que pour tout réel x > 0, g'(x) =\frac{x-1}{x^2}.
b. Étudier le sens de variation de la fonction g.
c. En déduire que pour tout réel x > 0, ln (x)\ge\frac{x-1}{x}.
Partie B: une méthode d'approximation de `$$ln(x)$
Neper choisit de prendre comme approximation de ln(x), la moyenne arithmétique des bornes de l'encadrement précédent , c'est-à-dire la moyenne des deux nombres \frac{x-1}{x} et x-1.
- Justifier que pour tout réel x > 0, ln(x)\approx \frac{1}{2}\left(x-\frac{1}{x}\right).
- a. Déduire de la question précédente une approximation de ln(0,99) et de ln (0,9995). Arrondir au cent-millième.
b. Comparer les valeurs obtenues avec celles données par la calculatrice. - Voici comment Neper a procédé pour obtenir son approximation de ln(0,7).
a. Vérifier, à l'aide de la calculatrice, que :
0,99^{36}\times 0,9995^{10}\le 0,7\le 0,99^{35}\times 0,9995^9
b. Justifier que:
36ln(0,99)+10ln(0,9995)\le ln(0,7)\le35ln(0,99)+9ln(0,9995)
c. Déduire des questions précédentes un encadrement d'amplitude un millième du nombre ln(0,7).
5. Suites géométriques et placement
Durant la Renaissance, le commerce se développant, les marchands ont été amenés à constituer des tables d'intérêts. Luca Pacioli (1447-1517), religieux franciscain,
mathématicien et fondateur de la comptabilité, présente la règle des 72 en 1494 dans son ouvrage intitulé Summa dearithmet ica, geometria, de proportioni et de proportionalita.
Cette règle est une méthode pour estimer le temps de doublement d'un capital. Luca Pacioli estime que si un capital est placé au taux d'intérêt de t \% par période
(en général, années), il faut \frac{72}{t} périodes pour le doubler.
Nous allons appliquer la règle des 72, puis déterminer une autre approximation du
nombre de périodes nécessaires au doublement d'un capital.
Partie A: la règle des 72
t désigne un nombre réel strictement positif et n est un nombre entier naturel non nul.
- Utiliser la règle de Pacioli pour estimer le nombre n de périodes nécessaires pour doubler un capital lorsqu'il est placé à un taux d'intérêts composés de:
- t = 1\%
- t = 5\%
- t = 10\%
- Au bout de n années de placement au taux d'intérêt de t \%, le capital est multiplié par \left(1+ \frac{t}{100}\right)^n.
a. Dans chaque cas, déterminer, en utilisant la fonction ln, le plus petit nombre
entier naturel n tel que \left(1+\frac{t}{100}\right)^n\ge 2.- t = 1\%
- t=5\%
- t=10\%
b. Comparer ces résultats avec ceux obten us à la question 1.
Partie B: une autre estimation
- f et g sont les fonctions définie s sur l'intervalle [ 0; +\infty[ par :
f (x) = ln(1 + x) - x+ \frac{x^2}{2}
g( x)= ln(1 +x)-x
a. Étudier les variations des fonctions f et de g sur l'intervalle [ 0; +\infty[.
b. En déduire que pour tout réel x de l'intervalle [ 0; +\infty[, x - \frac{x^2}{2} \le ln(1+x)\le x. - Pour des petites valeurs de x, \frac{x^2}{2} étant très petit, on choisit d'utiliser l'approximation ln(1 + x)\approx x.
a. Justifier que le nombre de périodes nécessaires au doublement d'un capital
placé au taux de t \% (pour des petites valeurs de `$$t$) est environ égal à
\frac{70}{t}.
b. Que devient cette règle si l'on veut tripler le capital?
6. Loi de Kepler
Au début du XVIIe siècle, l'astronome Johannes Kepler a établi des lois physiques qui décrivent les propriétés du mouvement des planètes autour du soleil.
Pour une planète tournant autour du Soleil, il considère que sa trajectoire est circulaire. Il note T sa période de révolution et r le rayon de son orbite (c'est-à-dire le rayon du cercle que forme sa trajectoire). On donne dans une feuille de tableur les mesures ci-dessous.

- Reproduire la feuille de tableur dans un logiciel et compléter les colonnes D et E.
- Construire, avec le tableur, le nuage de points de coordonnées (ln (r ) ; ln(T)).
Quel type de courbe semble-t -on obtenir? - Insérer une courbe de tendance linéaire (clic droit sur les points du graphique) et faire afficher l'équation de la courbe. Arrondir le coefficient directeur de la
droite au dixième. - En déduire que 2ln(T) = 3ln(r) + k , où k est une constante à déterminer.
- Montrer que T s'exprime en fonction de r sous la forme T^2 = Kr^3, où K est une constante réelle à déterminer.
7. Intensité sonore
On note I l'intensité acoustique d'un bruit, mesurée en watts par mètre carré ($W. m^{-2}$).
Cette intensité acoustique mesure une puissance acoustique par unité de surface.
On note I_0 l'intensité acoustique sous laquelle un humain n'entend pas le bruit.
On a I_0 = 10^{-12}~W.m^{-2}.
L'intensité acoustique du bruit émis lors d'une conversation normale est I_C = 10^{-6}~W.m^{-2}.
Le seuil de la douleur, c'est-à -dire l'intensité au-delà de laquelle le bruit risque d'endommager le système auditif, est égal à I_d = 10 W.m^{-2}.
Pour comparer ces intensités acoustiques, dont les ordres de grandeur sont très différents, on définit le niveau sonore, noté L, par:
L=\frac{10}{ln(10)}ln\left(\frac{I}{I_0}\right).
L est exprimé en décibel (dB).
- Calculer le niveau sonore correspondant aux intensités I_0, I_C et I_d.
- Dans une cantine, on trouve que le niveau sonore est égal à 85~dB. Calculer l'intensité acoustique correspondant à ce bruit.
- Lors d'un concert piano -voix, le niveau sonore du piano seul est mesuré à 72 décibels et celui de la chanteuse seule à 68 décibels.
Sachant que les intensités de plusieurs sources sonores s'additionnent, quel est le niveau sonore du concert? - Le seuil de la douleur est à 120 décibels.
Calculer l'intensité sonore correspondante. - Dans une artère très fréquentée, grâce à des aménagements urbains, l'intensité du bruit émis par le trafic a été divisée par deux.
Calculer l'atténuation du bruit obtenue, en décibels.