I – Primitives d’une fonction
1. généralités
Définition
Soit f une fonction définie sur un intervalle I.
On dit que F est une primitive de f sur I si et seulement si F est dérivable sur I et \forall x\in I, F'(x)=f(x).
Exemple
- La fonction F_1:\mapsto 2x^2+2x-3 est-elle une primitive sur \mathbb{R} de la fonction f:x\mapsto 4x+2?
- La fonction F_2:\mapsto 2x^2+2x+10 est-elle une primitive sur \mathbb{R} de la fonction f?
1.F_1 étant une fonction polynômiale, elle est dérivable sur \mathbb{R}.
F_1'(x)=2\times 2x+2=4x+2=f(x)
Donc F_1 est une primitive de f sur \mathbb{R}.
2.F_2 étant une fonction polynômiale, elle est dérivable sur \mathbb{R}.
F_2'(x)=2\times 2x+2=4x+2=f(x)
Donc F_2 est une primitive de f sur \mathbb{R}.
Propriété
Soit f une fonction définie sur un intervalle I et F une primitive de f sur I.
L’ensemble des primitives de f sur I est constitué par les fonctions G définies sur I par G(x)=F(x)+c où c\in\mathbb{R}.
Remarque
On dit aussi que deux primitives d’une même fonction f sur un intervalle I diffèrent d’une constante.
Démonstration
Soit f une fonction définie sur un intervalle I et F une primitive de f sur I.
- Soit c\in \mathbb{R}. Posons \forall x\in I, G(x)=F(x)+c.
La fonction F étant dérivable sur I (puisque c’est une primitive de f), on peut affirmer que la fonction G est dérivable sur I.
De plus G'(x)=F'(x)+0=F'(x)=f(x).
Donc la fonction G est une primitive de f sur I.- Réciproquement, supposons que G est une primitive de f sur I.
On a donc \forall x\in I, G'(x)=f(x).
Soit la fonction U définie sur I par U(x)=G(x)-F(x).
Les fonction F et G étant dérivables sur I (puisque des primitives de f sur I), la fonction U est aussi dérivable sur I.
(U)'(x) =G'(x)-F'(x)=f(x)-f(x)=0
La fonction U est donc une fonction constante.
Donc \exists c\in \mathbb{R}, U(x)=c.
\exists c\in \mathbb{R}, G(x)-F(x)=c.
\exists c\in \mathbb{R}, G(x)=F(x)+c.
Propriété
Soit f une fonction définie sur un intervalle I.
Il existe une unique primitive F de f sur l’intervalle I telle que F\left(x_0\right)=y_0 où x_0 et y_0 sont des nombres réels donnés avec x_0\in I.
Démonstration
Existence d’une telle fonction
Soit F une primitive de f sur I.
La fonction G définie par \forall x\in I, G(x)=F(x)-F(x_0)+y_0.
G est dérivable sur I car F aussi.
G'(x)=F'(x)-0+0=F'(x)=f(x)
Donc G est une primitive de f.
De plus, `$$G(x_0)=F(x_0)-F(x_0)+y_0=y_0$Il existe bien une primitive G de f telle que G\left(x_0\right)=y_0
Unicité d’une telle fonction
Supposons qu’il existe deux fonctions G et H, primitives de f sur I et telles que G\left(x_0\right)=y_0 et H\left(x_0\right)=y_0.
Soit U la fonction définie sur I par \forall x \in I, U(x)=G(x)-H(x).
La fonction U est dérivable sur I car F et G le sont aussi.
On a alors:
U'(x)=G'(x)-H'(x)=f(x)-f(x)=0
Donc la fonction U est une fonction constante.
De plus, U(x_0)=G(x_0)-H(x_0)=y_0-y_0=0
Donc la fonction U est la fonction nulle.
Ainsi \forall x\in I, U(x)=0.
Et donc \forall x\in I, G(x)-H(x)=0.
Ou encore \forall x\in I, G(x)=H(x).Il n’existe donc bien qu’une seule primitive G de f sur l’intervalle I telle que G\left(x_0\right)=y_0
Exemple
Soit f la fonction définie sur \mathbb{R} par f(x)=2x-e^x.
Déterminer la primitive de la fonction f qui vaut en .
La primitive que l’on cherche est de la forme F(x)=x^2-e^x+c, avec c\in\mathbb{R}.
De plus, F(0)=0
donc 0^2-e^0+c=0
soit encore -1+c=0
Et donc c=1
La primitive cherchée est la fonction F:x\mapsto x^2-e^x+1.
2. Tableau des primitives des fonctions de référence
Dans le tableau ci-dessous, c désigne un nombre réel.
La fonction f définie sur I par Les primitives de f sur I sont définie par avec I= f(x)=k, avec k\in\mathbb{R} F(x)=kx+c \mathbb{R} f(x)=x, avec m\in\mathbb{R} et p\in\mathbb{R} F(x)=\frac{1}{2}x^2+c \mathbb{R} f(x)=x^2 F(x)=\frac{1}{3}x^3+c \mathbb{R} f(x)=x^n, avec n\in\mathbb{N}^* F(x)=\frac{1}{n+1}x^{n+1}+c \mathbb{R} f(x)=\frac{1}{x} ln(x)+c ]0;+\infty[ f(x)=\frac{1}{x^2} F(x)=-\frac{1}{x}+c ]-\infty;0[ ou ]0;+\infty[ f(x)=\frac{1}{\sqrt{x}} F(x)=2\sqrt{x}+c \mathbb{R}^*_+ f(x)=\cos x F(x)=\sin x+c \mathbb{R} f(x)=\sin x F(x)=-\cos x+c \mathbb{R} f(x)=e^x F(x)=e^x+c $$\mathbb{R}$$`
3. Un autre tableau
Propriété
Soit u une fonction dérivable sur un intervalle I.
La fonction f est difinie sur I par Les primitives de f sont Conditions sur u f(x)=2u'(x)u(x) F(x)=[u(x)]^2+c f(x)=\frac{u'(x)}{u(x)} F(x)=ln(u(x))+c u(x)>0 sur I f(x)=u'(x)e^{u(x)} F(x)=e^{u(x)}+c
Exemple
Soit f la fonction définie sur \mathbb{R} par f(x)=(1+x)e^{\frac{1}{2}x^2+x-1}.
Déterminer la primitve F de la fonction f définie sur \mathbb{R} telle que F(1)=2.
En posant u(x)= \frac{1}{2}x^2+x-1, on remarque que u'(x)=x+1.
Ainsi f(x)=u'(x)e^{u(x)}.
Donc F(x)=e^{u(x)}+c=e^{\frac{1}{2}x^2+x-1}+c
Or F(1)=2
Donc e^{\frac{1}{2}\times 1^2+1-1}+c=2
Soit e^{\frac{1}{2}}+c=2
C’est-à-dire c=2-e^{\frac{1}{2}}
Ainsi F(x)=e^{\frac{1}{2}x^2+x-1}+2-e^{\frac{1}{2}}
II – Equation différentielle
1. Généralité
Définition
Une équation différentielle est une équation dans laquelle l’inconnue est une fonction et dans laquelle interviennent des dérivées de cette fonction.
Exemple
L’équation y'=3y+5 est une équation différentielle dans laquelle l’inconnue y est une fonction.
- Vérifier que la fonction f définie sur \mathbb{R} par f(x)=2e^{3x}-\frac{5}{3} est une solution de cette équation différentielle.
- Y a-t-il d’autres solutions?
1.La fonction f est dérivable sur \mathbb{R}.
f'(x)=2\times 3 \times e^{3x}=6e^{3x}
3f(x)+5=3\left(2e^{3x}-\frac{5}{3}\right)+5=6e^{3x}-5+5=6e^{3x}
Donc \forall x\in \mathbb{R}, f'(x)=3f(x)+5
Ainsi f est bien une solution de l’équation différentielle y'=3y+5.
2.Par exemple, x\mapsto -\frac{5}{3} et x\mapsto 7e^{3x}-\frac{5}{3} sont aussi solution de l’équation différentielle y'=3y+5.
Remarque
Trouver toutes les primitives d’une fonction f sur un intervalle I, c’est résoudre l’équation différentielle y'=f sur I.
2. Résolution d’équations différentielles y'=ay+b avec a\in\mathbb{R} et b\in\mathbb{R}
Définition
Résoudre une équation différentielle sur un intervalle I, c’est trouver toutes les fonctions dérivables sur I qui sont solutions de cette équation.
Propriété
Soit a\in\mathbb{R}. Considérons l’équation différentielle (E): y'=ay.
Les solutions de l’équation (E) sont les fonctions définies sur \mathbb{R} par f_k(x)=ke^{ax} où k\in\mathbb{R}.
Démonstration
Nous allons démontrer cette propriété en deux temps:
1.Toutes les fonctions du type f_k(x)=ke^{ax} où k\in\mathbb{R} sont solutions de (E).
2.Toutes les solutions de (E) sont du type f_k(x)=ke^{ax} où k\in\mathbb{R}.1.Soit k\in\mathbb{R}. Soit f_k la fonction définie sur \mathbb{R} par f_k(x)=ke^{ax}.
La fonction f_k est dérivable sur \mathbb{R} car la fonction exponentielle l’est.
f_k'(x)=kae^{ax}=ake^{ax}=af_k(x)
Donc f_k est bien solution de (E).2.Soit g une solution de (E) sur \mathbb{R}.
On a donc \forall x\in \mathbb{R}, g'(x)=ag(x) ou encore g'(x)-ag(x)=0.
Posons \forall x\in \mathbb{R}, \phi(x)=\frac{g(x)}{e^{ax}}=g(x)e^{-ax}.
\phi est une fonction dérivable sur \mathbb{R} car les fonctions g et exponentielle le sont.
\phi'(x)=g'(x)e^{-ax}+g(x)\times (-a)e^{-ax}=e^{-ax}(g'(x)-ag(x))=e^{-ax}\times 0=0
Donc$$$\forall x\in \mathbb{R}, \phi'(x)=0$$[/katex]
La fonction \phi est donc une fonction constante.
\exists k\in\mathbb{R}, \forall x\in\mathbb{R}, \phi(x)=k
On a donc:
\frac{g(x)}{e^{ax}}=k soit encore g(x)=ke^{ax}
Donc les solutions de (E) sont de la forme f_k(x)=ke^{ax}.
Exemple
Résoudre l'équation différentielle (E):y'=4y.
Les solutions de l'équation (E) sont les fonctions définies sur \mathbb{R} par f_k(x)=ke^{4x} où k\in\mathbb{R}.
Définition
Soient a\in\mathbb{R} et b\in\mathbb{R}. Considérons l'équation différentielle (E): y'=ay+b.
L'équation différentielle (H_E):y'=ay est appelée équation homogène de l'équation différentielle (E).
Méthode de résolution de l'équation différentielle y'=ay+b
- Résoudre l'équation homogène y'=ay.
- Trouver une solution particulière constante de l'équation différentielle y'=ay+b
- A chaque solution de l'équation homogène, ajouter la solution particulière précédente. Cela donnera l'ensemble des fonctions solutions de l'équation y'=ay+b. On les appelle solution générale de l'équation `$$y'=ay+b$
Propriété
Soient a\in\mathbb{R} et b\in\mathbb{R}. Considérons l'équation différentielle (E): y'=ay+b.
Les solutions de l'équation (E) sont les fonctions f_k définies sur \mathbb{R} par f_k(x)=ke^{ax}-\frac{b}{a}.
Propriété
Soient a\in\mathbb{R} et b\in\mathbb{R}.
Considérons l'équation différentielle (E): y'=ay+b sur un intervalle I.
Soit y_0 \in\mathbb{R} et x_0\in I.
Il existe une unique solution F de (E) sur I telle que F\left(x_0\right)=y_0
Exemple
- Résoudre dans \mathbb{R} l'équation différentielle (E): y'= 2y-3.
- Parmis toutes les solutions de (E), trouver celle qui vaut \frac{5}{2} en \frac{1}{2}.
L'équation homogène de (E) est (H):y'=2y.
Les solutions de (H) sont les fonctions f_k définies sur \mathbb{R} par f_k(x)=ke^{2x} avec k\in\mathbb{R}.Cherchons une solution particulière constante g de (E).
Si g est constante, sa dérivée g' est nulle donc on a:
g'(x)=2g(x)-3
0=2g(x)-3
g(x)=\frac{3}{2}
La solution particulière constante est la fonction g définie par \forall x\in \mathbb{R}, g(x)=\frac{3}{2}.Les solutions de (E) sont donc les fonctions g_k définies sur \mathbb{R} par \forall x\in \mathbb{R}, g_k(x)=f_k(x)+g(x)=ke^{2x}+\frac{3}{2}
- Cherchons k tel que g_k(\frac{1}{2})=\frac{5}{2}
ke^{2\times \frac{1}{2}}+\frac{3}{2}=\frac{5}{2}
ke^1=\frac{5}{2}-\frac{3}{2}
ke=1
k=\frac{1}{e}Donc la solution de (E) telle que g_k(\frac{1}{2})=\frac{5}{2} est g_{\frac{1}{e}} définie par g_{\frac{1}{e}}(x)=\frac{1}{e}e^{2x}+\frac{3}{2}=e^{2x-1}+\frac{3}{2}
3. Allure des courbes solutions
- Cas où a > 0

- Cas où a < 0

III - Quelques problèmes
1. Loi de décroissance radioactive
À l'échelle macroscopique, des expériences de comptage permettent de conjecturer que le nombre moyen de noyaux radioactifs d'un échantillon qui se désintègrent sur une courte durée est proportionnel, à la fois au nombre de noyaux présents à l'instant initial et à la durée d'observation selon la relation:
(1) \frac{N(t+\Delta t)-N(t)}{\Delta t} =-\lambda N(t) avec \lambda \in\mathbb{R}_+^* qui dépend de l'élément étudié.
Dans cette relation, t désigne un instant ($t \ge 0$$), [/katex]$$\Delta t$$ la durée de l'observation ($\Delta t > 0$$[/katex] proche de zéro), N(t) (resp. N(t + \Delta t)) le nombre de noyaux de l'échantillon à l'instant t (resp. à l'instant t + \Delta t).
Lorsque \Delta t tend vers zéro, la relation (1) s'écrit alors sous forme de l'équation différentielle (E):
N'(t) = -\lambda N(t)
Nous allons étudier cette loi de décroissance radioactive lorsque \Delta t tend vers , c'est-à-dire en envisageant un modèle continu. Dans un second temps, on applique ce modèle à la datation au carbone 14.
- Équation différentielle
a. On note N(0) = N_0 le nombre de noyaux à l'instant initial t = 0.
Exprimer les solutions sur [0 ; + \infty[ de (E) en fonction de N_0 et \lambda.
b. La demi-vie d'un élément radioactif est la durée D au bout de laquelle la moitié des noyaux de l'échantillon s'est désintégrée.
Exprimer \lambda en fonction de la demi-vie D d'un élément.
c. Voici une fonction Lambda ci-dessous, écrite en langage Python.from math import log def lambda(D): L=log(2)/D return L[/katex]Expliquer le rôle de ce programme.
d. Saisir ce programme et l'exécuter afin d'obtenir les valeurs de \lambda pour les éléments radioactifs du tableau ci-dessous.Elément Demi-vie (en années) Uranium 238 4,5\times 10^9 Plutonium 239 2,4\times 10^4 Carbone 14 5730 Iode 131 0,022 - Datation au carbone 14
Les organismes vivants contiennent naturellement du carbone 14.
La proportion de carbone 14 (~^{14}C) par rapport au carbone 12 (~^{12}C) présent dans un organisme vivant est constante, mais à la mort de cet organisme, le ~^{14}C qu'il contient se désintègre.
a. On a découvert dans une grotte en Dordogne un foyer contenant du charbon de bois. À quantité égale, un morceau de bois actuel contient 1,5 fois plus de ~^{14}C que celui prélevé dans la grotte.
Estimer une datation de l'occupation de la grotte.
b. Lorsque la teneur en ~^{14}C d'un organisme devient inférieure à 0,3\% de sa valeur initiale, on ne peut plus dater précisément à l'aide du ~^{14}C.
Saisir puis compléter le programme ci-dessous écrit en langage Python, afin de déterminer l'âge à partir duquel un organisme ne peut plus être daté au ~^{14}C.from math import exp def duree(p): t=0 while exp(......)> ....... : t=t+1 return t[/katex]
2. Charge d'un condensateur
Un condensateur est un dipôle constitué de deux lames métalliques séparées par un isolant. Il est schématisé 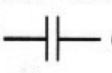 dans un circuit électrique.
dans un circuit électrique.
Il permet d'emmagasiner de l'énergie électrique pendant un certain temps, puis de décharger cette énergie.
Ce principe est, par exemple, utilisé lorsqu'on charge, puis que l'on déclenche le flash d'un appareil photo.
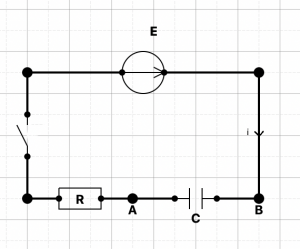
Un circuit électrique comprend un générateur de force électromotrice E, un dipôle constitué d'une résistance R, d'un condensateur C et d'un interrupteur.
À tout instant t \ge 0, en seconde, on note:
- i(t) l'intensité , en ampère, dans le circuit.
- q(t) la charge, en coulomb, du condensateur et u(t) la tension , en volt,
à ses bornes. Ils sont liés par la relation q(t) = Cu(t) où C est la capacité du condensateur, en farad.
On sait que:
- la tension E, en V, aux bornes du générateur est égale à la somme des
tensions aux bornes du condensateur et de la résistance, soit E = u(t) + Ri(t). - la charge du condensateur et l'intensité du courant produit lors de la fermeture de l'interrupteur sont liées par la relation i(t) = q'(t).
Nous allons étudier l'évolution de la capacité de charge électrique du condensateur dans le temps , et en fonction de l'intensité du courant traversant le circuit.
- Etude de la charge du condensateur
a. Expliquer pourquoi la charge q du condensateur vérifie l'équation différentielle (E):
$Rq'+\frac{1}{C}q=E$$`
b. Résoudre (E) sur [0 ;+\infty[.
c. On suppose que q(0) = 0, c'est-à-dire que le condensateur est sans charge initiale.
Exprimer q(t) en fonction de t.
d. La charge maximum du condensateur est le nombre Q égal à la limite de la fonction q en +\infty. Calculer Q.
e. Dresser le tableau de variations de la fonction q sur l'intervalle [O; +\infty[. - Pourcentage de sa charge maximum
On note \tau = RC.
a. Déterminer l'expression de q(t) en fonction de Q et de \tau.
b. La fonctionduree[/katex] ci-dessous, écrite en langage Python, permet d'obtenir
la durée de charge nécessaire pour que le condensateur soit chargé à p\% de sa charge maximum lorsque R = 100\Omega, C = 1 F et E = 5 V.from math import exp def duree(p): t=0 while 1-exp(......) < ...... : t=t+1 return t[/katex]Compléter la ligne 5.
Saisir ce programme et l'exécuter pour p égal à:- 10\%
- 50\%
- 90\%
- Etude de l'intensité du courant `$$t$
Expliquer pourquoi, pour tout t \ge 0, i(t) = \frac{E}{R}e^{-\frac{t}{\tau}}.
Dresser le tableau de variations de la fonction i.
3. Chute d'un corps dans un fluide visqueux
On dispose d'un liquide visqueux de masse volumique \rho = 1 000 kg.m^{-3}.
À la date t = 0, on dépose une fine couche de particules solides de forme sphérique, de masse volumique \rho_S = 1500 kg.m^{-3} et de masse m = 4,5 \times 10^{-14}~kg.
Les part icules que l'on suppose initialement au repos, se déplacent verticalement vers le fond du récipient. Elles sont soumises à leur poids \overrightarrow{P} vertical vers le bas, à la poussée d'Archimède \overrightarrow{\pi} verticale vers le haut et à une force de frottement
colinéaire à la vitesse \overrightarrow{v}, de sens contraire et de valeur F = kv, avec k = 3,1 \times 10^{- 12}~kg.s^{-1}.
Nous allons étudier la vitesse de chute d'une particule dans ce liquide visqueux à l'aide d'une équation différentielle.
La deuxième loi de Newton entraîne l'égalité vectorielle \overrightarrow{P}+ \overrightarrow{F}+ \overrightarrow{\pi}= m\overrightarrow{a}, ce qui conduit à l'équation différentielle vérifiée par la vitesse v de la particule:
$mv'=mg-kv-mg\frac{\rho}{\rho_S}$
- Équation différentielle
a. Expliquer pourquoi la vitesse v de la particule vérifie l'équation différentielle (E):
$v'+\frac{k}{m}v=g\left(1-\frac{\rho}{\rho_S}\right)$$`
b. Déterminer des arrondis au millième de \frac{k}{m} et g\left(1-\frac{\rho}{\rho_S}\right).
On prend g=9,81~N.kg^{-1}.
c. Expliquer pourquoi v(0) = 0.
En déduire l'expression de la fonction v. - Etude de la vitesse de la particule
a. La vitesse limite de la particule, notée v_{l}, est obtenue lorsque v' (t)= 0.
Déterminer cette vitesse limite. Arrondir au millième.
b. Expliquer pourquoi pour tout réel t \ge 0 , v(t) = v_l \left(1- e^{-\frac{k}{m}t}\right).
c. Dresser le tableau de variations de la fonction v.
d. Dans un repère orthonormé, déterminer l'équation de la tangente T à la courbe représentative \mathscr{C} de v au point d'abscisse 0.
e. Dans un repère orthonormé d'unité 2 cm pour 0,01~s en abscisse et 2 cm pour 0,01~m.s^{-1} en ordonnée, représenter T, \mathscr{C} et tracer l'asymptote horizontale \Delta à \mathscr{C}. - Détermination du temps caractéristique
Le temps caractéristique, noté \tau, est l'abscisse du point d'intersection de T et \Delta.
a. Lire une valeur approchée de ce temps caractéristique sur le graphique construit à la question 2.e.
b. Démontrer que v'(0) = v_l \times \frac{k}{m}, puis que \tau=\frac{m}{k}.
c. En déduire le temps caractéristique \tau. Arrondir au millième.
4. Dynamique des populations: modèles continus de Malthus et de Verhulst
On observe une populat ion de jaguars dans une réserve naturelle.
On note N(t) le nombre d'individus, en millier, présents au sein de la réserve en fonction du temps, en année.
N_0 = N(0) désigne le nombre d'individus à l'ouverture de la réserve.
Ces animaux étant quasiment menacés d'extinction, leur nombre à l'ouverture de la réserve est faible et leur protection, ainsi que celle de leur habitat, laissent espérer une croissance de la population.
Nous allons étudier l'évolution de cette population de jaguars dans le temps. Pour cela, on envisage deux modélisations (de Malthus et de Verhulst) à l'aide d'équations différentielles.
- Le modèle de Malthus
Selon le modèle de Malthus, la fonction N_1 est la solution de l'équation différentielle (M) : N' = rN où r est une constante strictement positive appelée « taux de croissance de la population ».
a. Résoudre (M) sur [ 0; +\infty[.
b. Déterminer la limite de N_1 en +\infty.
c. Expliquer l'incohérence de ce modèle. - Le modèle de Verhulst
Selon le modèle de Verhulst, la fonction N_2 est la solution de l'équation différentielle (V) : N' = rN\left( 1- \frac{N}{K} \right) où r est le taux de croissance précédent et K est une constante strictement positive.
a. Démontrer que la fonction N_2 définie sur [0 ;+ \infty[ par N_2(t) = \frac{N_0K}{N_0+\left(K-N_0\right)e^{-rt}} est solution de (V) et que N_2(0)= N(0). Déterminer la limite de N_2 en +\infty.
b. Utiliser (V) pour étudier le signe de la dérivée N_2'(t) et en déduire le tableau de variations de N_2. - Comparaison des modèles et seuil
Voici un programme incomplet écrit en langage Python qui indique le nombre d'années pour que la population dépasse un seuil S. On prend r = 0,05, N_0 = 10, K = 400.from math import exp def seuil(S): t=0 while ...... < S: t=t+1 M="Seuil de Malthus = " n=0 while ...... < S: n=n+1 V="Seuil de Verhulst = " return (M,t,V,n)[/katex]a. Compléter ce programme.
Saisir ce programme et l'exécuter pour S = 200, puis S = 350.
b. Interpré ter ces résultats.