Chapitre 07 – Calculs d’aires

I – Intégrale d’une fonction continue et positive sur un intervalle

---

1. Unité d’aire

---

Définition

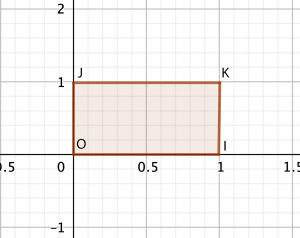
Soit un repère orthogonal \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right).
L’unité d’aire, notée u.a., est l’aire du rectangle OIKJ où K(1;1).

2. Aire sous la courbe représentative d’une fonction continue et positive sur un intervalle

---

Définition

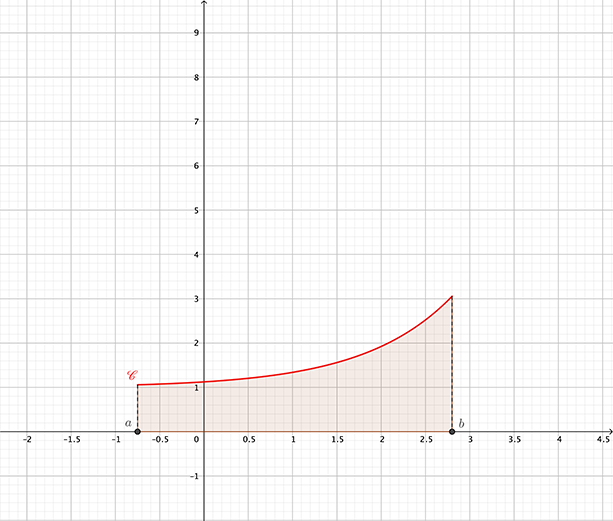
Soit \mathscr{C} une courbe représentative dans un repère orthogonal \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right) d’une fonction continue et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a < b.
Le domaine délimité par la courbe \mathscr{C}, l’axe des abscisses et les droites d’équations x=a et x=b est appelé aire sous la courbe \mathscr{C}.

3. Intégrale de a à b d’une fonction continue et positive sur un intervalle

---

Définition

Soit f une fonction continue et positive sur un intervalle [a;b], avec a\in\mathbb{R} et b\in\mathbb{R}. Soit \mathscr{C} sa courbe représentative dans un repère orthogonal \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right).
L’aire, exprimée en u.a., du domaine situé sous la courbe \mathscr{C} est appelé intégrale de a à b de la fonction f. Elle est notée \int_{a}^{b} f(x) \mathrm{d}x.

Remarque

• Pour toute fonction continue et positive sur l’intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a < b, \int_{a}^{b} f(x) \mathrm{d}x\ge 0.
• \int_{a}^{b} f(x) \mathrm{d}x ne dépend que de f et de [a;b]. Il est indépendant du choix des unités sur les axes.
• On dit que x est une variable muette car elle ne se retrouve pas dans le résultat. On peut donc noter indifféremment \int_{a}^{b} f(x) \mathrm{d}x=\int_{a}^{b} f(t) \mathrm{d}t=\int_{a}^{b} f(u)\mathrm{d}u=....

Propriété

Soit f une fonction continue et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a< b.

• `$$\int_{a}^{a} f(x) \mathrm{d}x=0$
• Pour tous réels c, d, e de l’intervalle [a;b], \int_{c}^{d} f(x)\mathrm{d}x+\int_{d}^{e} f(x) \mathrm{d}x=\int_{c}^{e} f(x) \mathrm{d}x. (cette relation est appelée relation de Chasles).
• On peut parfois profiter de l’invariance de l’aire par translation ou symétrie.

Exemple

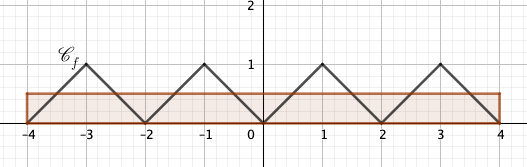
Soit f la fonction définie sur l’intervalle [-4;4], représentée dans le repère ci-dessous.

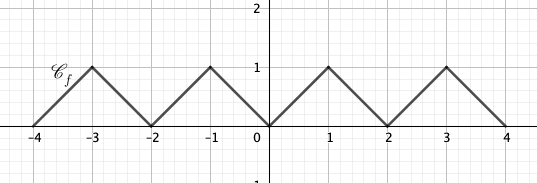
Calculer \int_{-4}^{4} f(x) \, \mathrm{d}x.

Les deuxièmes et troisièmes triangles ont la même aire puisqu’ils sont symétriques par rapport à l’axe des ordonnées.
Donc \int_{-2}^{0} f(x) \, \mathrm{d}x=\int_{0}^{2} f(x) \, \mathrm{d}x.
Les premier et quatrièmes triangles sont les images du troisième triangle par translation.
Donc \int_{-4}^{-2} f(x) \mathrm{d}x=\int_{0}^{2} f(x) \mathrm{d}x et \int_{2}^{4} f(x)\mathrm{d}x=\int_{0}^{2} f(x)\mathrm{d}x.
Ainsi \int_{-4}^{4} f(x) \mathrm{d}x=\int_{-4}^{-2} f(x) \mathrm{d}x+\int_{-2}^{0} f(x) \mathrm{d}x+\int_{0}^{2} f(x) \mathrm{d}x+\int_{2}^{4} f(x) \mathrm{d}x
\int_{-4}^{4} f(x) \mathrm{d}x=\int_{0}^{2} f(x) \mathrm{d}x+\int_{0}^{2} f(x) \mathrm{d}x+\int_{0}^{2} f(x) \mathrm{d}x+\int_{0}^{2} f(x) \mathrm{d}x
\int_{-4}^{4} f(x) \mathrm{d}x=4\int_{0}^{2} f(x) \mathrm{d}x
\int_{-4}^{4} f(x) \mathrm{d}x=4\times \frac{2\times 1}{2}=4

4. Valeur moyenne d’une fonction sur un intervalle

---

Définition

Soit f une fonction continue et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a < b.
La valeur moyenne de la fonction f sur [a;b] est le nombre réel \mu tel que:
\mu=\frac{1}{b-a}\int_{a}^{b} f(x) \mathrm{d}x

Exemple

Soit f la fonction définie sur l’intervalle [-4;4], représentée dans le repère ci-dessous.

1. Déterminer la valeur moyenne de f sur [-4;4].
2. Interprêter graphiquement.

1.\mu=\frac{1}{4-(-4)}\int_{-4}^{4} f(x) \mathrm{d}x=\frac{1}{8}\times 4=\frac{1}{2}
2.Graphiquement, l’aire sous la courbe est égale à l’aire d’un rectangle de largeur b-a=8 et de hauteur \mu=\frac{1}{2}

Remarque

Soit f une fonction continue et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a < b.
Soient m le minimum de f sur [a;b] et M le maximum de f sur [a;b].
La valeur moyenne de f sur sur [a;b] est comprise entre m et M: m\le \mu\le M.

On remarque m\le \mu\le M.
On peut le démontrer facilement puisque l’aire du rectangle bleu est inférieure ou égale à l’aire sous la courbe \mathscr{C} et l’aire du rectangle gris est supérieure ou égale à l’aire sous la courbe \mathscr{C}.
On peut donc écrire m(b-a)\le \int_{a}^{b} f(x) \mathrm{d}x\le M(b-a).
Soit m\le \frac{1}{b-a}\int_{a}^{b} f(x) \mathrm{d}x\le M.
Ou encore m\le \mu\le M.

II – Approximation d’une intégrale d’une fonction continue positive croissante

---

Méthode des rectangles

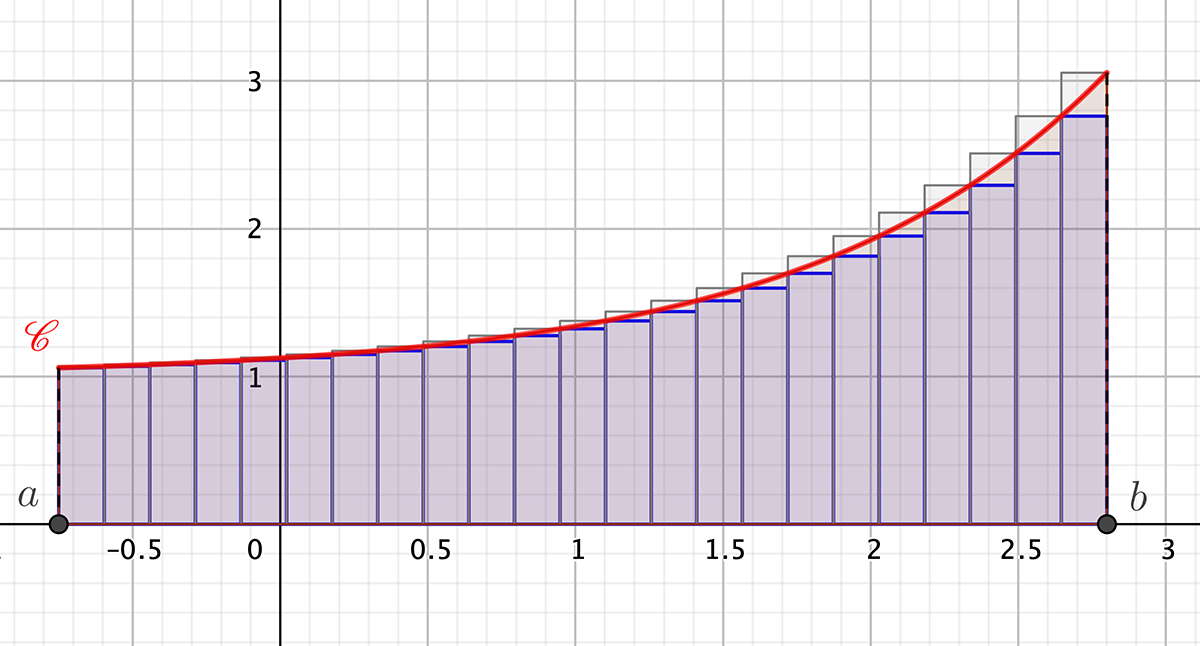
Soit f une fonction continue, croissante et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a< b.
Soit \mathscr{C} sa courbe représentative dans un repère orthogonal \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right).

• On subdivise l’intervalle [a;b] en n intervalles de même longueur h=\frac{b-a}{n} et on note x_k=a+kh avec k un nombre entier tel que 0\le k\le n.
• Sur chaque intervalle \left[x_k;x_{k+1}\right] (0\le k\le n-1), on construit les rectangle de hauteurs f(x_k) et f(x_{k+1}).

On appelle s_n la somme des aires, en u.a., des rectangles bleus contenus dans le domaine sous la courbe \mathscr{C}.
On appelle S_n la somme des aires, en u.a., des rectangles gris qui contiennent le domaine sous la courbe \mathscr{C}.

Propriété

Soit f une fonction continue, croissante et positive sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a < b.
\forall n\in\mathbb{N}^*, s_n\le \int_{a}^{b} f(x) \mathrm{d}x \le S_n
avec s_n=\frac{b-a}{n}\left(f(x_0)+f(x_1)+...+f(x_{n-1})\right)=\frac{b-a}{n}\displaystyle \sum_{k=0}^{n-1} f(x_k)
et s_n=\frac{b-a}{n}\left(f(x_1)+f(x_2)+...+f(x_n)\right)=\frac{b-a}{n}\displaystyle \sum_{k=1}^{n} f(x_k)

Remarque

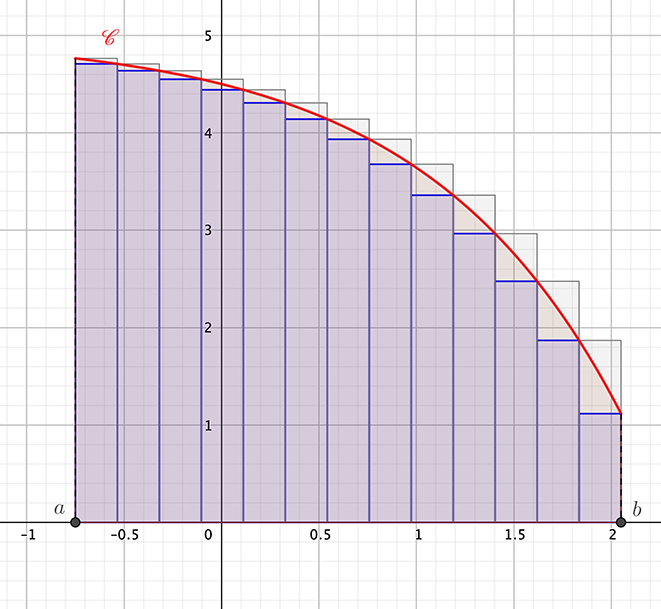
Dans le cas où f une fonction continue, décroissante et positive sur un intervalle [a;b], on échange les valeur de s_n et S_n.

Remarque

Dans le cadre de la propriété, on remarque que:
S_n-s_n=\frac{b-a}{n}\left(f(x_n)-f(x_0)\right)
Ainsi \lim \limits_{n\rightarrow +\infty} S_n-s_n=0 car f(x_n)= M avec M le maximum de f sur [a;b].
Ce qui veut dire que plus n augmente plus l’encadrement de \int_{a}^{b} f(x) \mathrm{d}x a une amplitude petite.
Et donc \lim \limits_{n\rightarrow +\infty} S_n=\lim \limits_{n\leftarrow +\infty} s_n=\int_{a}^{b} f(x) \mathrm{d}x (hors programme)

Exemple

Soit la fonction exponentielle définie sur [0;1] par f(x)=e^x.

1. Rappeler le sens de variation de la fonction exponentielle.
2. En déduire un encadrement de \int_{0}^{1} e^x \mathrm{d}x par la méthode des rectangles:
   a. en subdivisant l’intervalle en 10.
   b. en subdivisant l’intervalle en 100.
3. Conjecturer la valeur de \int_{0}^{1} e^x \mathrm{d}x.
4. Démontrer que \forall n\in\mathbb{N}, \frac{e-1}{n\left(e^{\frac{1}{n}}-1\right)}\le \int_{0}^{1} e^x \mathrm{d}x\le \frac{e-1}{n\left(1-e^{-\frac{1}{n}}\right)}.
5. a. Démontrer que \lim\limits_{x\rightarrow 0} \frac{e^x-1}{x}=1.
   b. En déduire que \lim\limits_{n\rightarrow +\infty} n\left(e^{\frac{1}{n}}-1\right)=1.
   c. De même, démontrer que \lim\limits_{n\rightarrow +\infty} n\left(1-e^{-\frac{1}{n}}\right)=1.
6. En déduire la valeur de \int_{0}^{1} e^x \mathrm{d}x.

1.~ La fonction exponentielle est croissante sur [0;1].
2.a. De plus, \forall x\in [0;1], e^x > 0.
Donc d’après la méthode des rectangles,
s_{10}\le \int_{a}^{b} f(x) \mathrm{d}x \le S_{10}
avec :
s_{10}=\frac{1-0}{10}f(x_0)+\frac{1-0}{10}f(x_1)+...+\frac{1-0}{10}f(x_{9})=\frac{1}{10}(f(x_0)+f(x_1)+...+f(x_{9}))
S_{10}=\frac{1-0}{10}f(x_1)+\frac{1-0}{10}f(x_2)+...+\frac{1-0}{10}f(x_{10})=\frac{1}{10}(f(x_1)+f(x_2)+...+f(x_{10}))
\forall k\in\mathbb{N}, tel que 0\le k\le n, x_k=0+\frac{1-0}{10}\times k=\frac{k}{10}
Donc \forall k\in\mathbb{N}, tel que 0\le k\le n, f(x_k)=f(\frac{k}{10})=e^{\frac{k}{10}}=\left(e^{\frac{1}{10}}\right)^k.
Ainsi s_{10}=\frac{1}{10}\left[\left(e^{\frac{1}{10}}\right)^0+\left(e^{\frac{1}{10}}\right)^1+...+\left(e^{\frac{1}{10}}\right)^9\right]
s_{10}=\frac{\left(e^{\frac{1}{10}}\right)^{10}-1}{10\left(e^{\frac{1}{10}}-1\right)}=\frac{e-1}{10\left(e^{\frac{1}{10}}-1\right)}
De même, S_{10}=e^{\frac{1}{10}}\frac{\left(e^{\frac{1}{10}}\right)^{10}-1}{10\left(e^{\frac{1}{10}}-1\right)}=\frac{e^{\frac{1}{10}}(e-1)}{10\left(e^{\frac{1}{10}}-1\right)}
On a donc \frac{e-1}{10\left(e^{\frac{1}{10}}-1\right)} \le \int_{0}^{1} e^x \mathrm{d}x \le \frac{e^{\frac{1}{10}}(e-1)}{10\left(e^{\frac{1}{10}}-1\right)}
b. De même, on obtient:
\frac{e-1}{100\left(e^{\frac{1}{100}}-1\right)} \le \int_{0}^{1} e^x \mathrm{d}x \le \frac{e^{\frac{1}{100}}(e-1)}{100\left(e^{\frac{1}{100}}-1\right)}
3.~ Il semblerait que \int_{0}^{1} e^x \mathrm{d}x=e-1.
4.~ Soit n\in\mathbb{N}^*. Subdivisons en n l’intervalle [0;1].
On a x_k=0+k\frac{1-0}{n}=\frac{k}{n}
s_n=\frac{1-0}{n}(f(x_0)+f(x_1)+...+f(x_{n-1}))
s_n=\frac{1}{n}\left[\left(e^{\frac{1}{n}}\right)^0+\left(e^{\frac{1}{n}}\right)^1+...+\left(e^{\frac{1}{n}}\right)^{n-1}\right]
s_n=\frac{1}{n}\left(\frac{\left(e^{\frac{1}{n}}\right)^n-1}{e^{\frac{1}{n}}-1}\right)
s_n=\frac{1}{n}\left(\frac{e-1}{e^{\frac{1}{n}}-1}\right)
s_n=\frac{e-1}{n\left(e^{\frac{1}{n}}-1\right)}
~
S_n=\frac{1-0}{n}(f(x_1)+f(x_2)+...+f(x_{n}))
S_n=\frac{1}{n}\left[\left(e^{\frac{1}{n}}\right)^1+\left(e^{\frac{1}{n}}\right)^2+...+\left(e^{\frac{1}{n}}\right)^{n}\right]
S_n=\frac{1}{n}\left(e^{\frac{1}{n}}\times \frac{\left(e^{\frac{1}{n}}\right)^n-1}{e^{\frac{1}{n}}-1}\right)
S_n=\frac{1}{n}\left(\frac{e^{\frac{1}{n}}(e-1)}{e^{\frac{1}{n}}-1}\right)
S_n=\frac{e^{\frac{1}{n}}(e-1)}{n\left(e^{\frac{1}{n}}-1\right)}
Donc \forall n\in\mathbb{N}, \frac{e-1}{n\left(e^{\frac{1}{n}}-1\right)}\le \int_{0}^{1} e^x \mathrm{d}x\le \frac{e-1}{n\left(1-e^{-\frac{1}{n}}\right)}
5.a. La fonction exponentielle est dérivable sur [0;1] donc:
\lim\limits_{x\rightarrow 0} \frac{e^x-1}{x}=\lim\limits_{x\rightarrow 0} \frac{exp(x)-exp(0)}{x-0}=exp'(0)=exp(0)=1
b. \lim\limits_{n\rightarrow +\infty} n\left(e^{\frac{1}{n}}-1\right)=\lim\limits_{n\rightarrow +\infty} \frac{\left(e^{\frac{1}{n}}-1\right)}{\frac{1}{n}}=\lim\limits_{x\rightarrow 0} \frac{e^x-1}{x}=1 avec le changement de variable x=\frac{1}{n} et \lim\limits_{n\rightarrow +\infty} \frac{1}{n}=0
c. \lim\limits_{n\rightarrow +\infty} n\left(1-e^{-\frac{1}{n}}\right)=\lim\limits_{n\rightarrow +\infty} \frac{e^{-\frac{1}{n}}\left(e^{\frac{1}{n}}-1\right)}{\frac{1}{n}}
Or \lim\limits_{n\rightarrow +\infty} e^{-\frac{1}{n}}=1 et \lim\limits_{n\rightarrow +\infty} \frac{\left(e^{\frac{1}{n}}-1\right)}{\frac{1}{n}}=1 donc \lim\limits_{n\rightarrow +\infty} n\left(1-e^{-\frac{1}{n}}\right)=1
6.~ \lim\limits_{n\rightarrow +\infty} s_n= \lim\limits_{n\rightarrow +\infty}\frac{e-1}{n\left(e^{\frac{1}{n}}-1\right)}=e-1
\lim\limits_{n\rightarrow +\infty} S_n= \lim\limits_{n\rightarrow +\infty}\frac{e^{\frac{1}{n}}(e-1)}{n\left(e^{\frac{1}{n}}-1\right)}=e-1
Or \forall n\in \mathbb{N}^*, s_n\le \int_{0}^{1} e^x \mathrm{d}x\le S_n
Donc \int_{0}^{1} e^x \mathrm{d}x=e-1, d’après le théorème des gendarmes.

III – Intégrale d’une fonction continue de signe quelconque sur un intervalle

---

1. Expression d’une primitive à l’aide d’une intégrale

---

Théorème

Soit f une fonction continue sur un intervalle I. Soit a \in I.
La fonction F_a:x\in I\mapsto \int_{a}^{x} f(t) \mathrm{d}t est la primitive de la fonciton f sur I telle que F_a(a)=0.

Démonstration

On ne s’intéressera dans cette démonstration, qu’au cas où f est une fonction continue positive croissante.
Soit x_0 et h deux nombres réels tels que x_0\in[a;b] et x_0+h\in[a;b].

1er cas: h>0.
F_a(x)=\int_{a}^{x} f(x) \mathrm{d}x
Donc F_a(x_0+h)=\int_{a}^{x_0+h} f(t) \mathrm{d}t=\int_{a}^{x_0} f(t) \mathrm{d}t+\int_{x_0}^{x_0+h} f(t) \mathrm{d}t=F_a(x_0)+\int_{x_0}^{x_0+h} f(t) \mathrm{d}t
D’où F_a(x_0+h)-F_a(x_0)=\int_{x_0}^{x_0+h} f(t) \mathrm{d}t
Or la fonction f est croissante continue et positive, donc:
\forall x\in[x_0;x_0+h], f(x_0)\le f(x)\le f(x_0+h).
Ainsi, f(x_0)(x_0+h-x_0)\le \int_{x_0}^{x_0+h} f(t)\le f(x_0+h)(x_0+h-x_0)
Ou encore hf(x_0)\le \int_{x_0}^{x_0+h} f(t)\le hf(x_0+h).
On a encore hf(x_0)\le F_a(x_0+h)-F_a(x_0)\le hf(x_0+h).
Ce qui peut s’écrire f(x_0)\le \frac{F_a(x_0+h)-F_a(x_0)}{h}\le f(x_0+h)
Or \lim \limits_{h\rightarrow 0} f(x_0+h)=f(x_0) car f est continue en x_0.
Donc d’après le théorèmes des gendarmes, on a:
\lim \limits_{h\rightarrow 0}\frac{F_a(x_0+h)-F_a(x_0)}{h}=f(x_0)
Ainsi F_a est dérivable en x_0 et F_a'(x_0)=f(x_0).

2ème cas: h<0
De même mais on aura, après calculs: f(x_0+h)\le \frac{F_a(x_0+h)-F_a(x_0)}{h}\le f(x_0)

\forall x_0\in[a;b], F_a est dérivable en x_0 et F_a'(x_0)=f(x_0).
Donc F_a est dérivable sur [a;b] et \forall x\in[a;b], F_a'(x)=f(x).
F_a est donc bien une primitive de f sur [a;b].
De pus, F_a(a)=0 donc F_a est bien la primitive de f qui s’annule en a.

Exemple

Soit x\in\mathbb{R}. Déterminer \int_{-2}^{x} t^3 \mathrm{d}t.

\int_{-2}^{x} t^3 \mathrm{d}t est la primitive de la fonction cube qui s’annule en -2.
Or une primitive de la fonction cube est définie par:
F(x)=\frac{1}{3+1}x^{3+1}+C=\frac{1}{4}x^4+C avec C\in\mathbb{R}.
Or F(-2)=0 donc \frac{1}{4}(-2)^4+C=0
Soit 4+C=0 ou encore C=-4.
On a donc \int_{-2}^{x} t^3 \mathrm{d}t=\frac{1}{4}x^4-4

Propriété

Soit F une primitive d’une fonction f continue sur l’intervalle I. Soient a\in I et b\in I. On a:
\int_{a}^{b} f(x) \mathrm{d}x=F(b)-F(a) que l’on note aussi \int_{a}^{b} f(x) \mathrm{d}x=\left[F(x)\right]_a^b.

Exemple

Calculer \int_{-2}^{4} x^3 \mathrm{d}x.

Une primitive de la fonction cube sur \mathbb{R} est la fonction F définie par F(x)=\frac{1}{4}x^4.
Donc \int_{-2}^{4} x^3 \mathrm{d}x=\left[\frac{1}{4}x^4\right]_{-2}^4=F(4)-F(-2)=\frac{1}{4}\times 4^4-\frac{1}{4}\times (-2)^4=64-4=60

Propriété

Soit f une fonction continue sur l’intervalle I. Soient a\in I et b\in I. On a:
\int_{b}^{a} f(x) \mathrm{d}x=-\int_{a}^{b} f(x) \mathrm{d}x

Exemple

Calculer \int_{4}^{-2} x^3 \mathrm{d}x.

\int_{4}^{-2} x^3 \mathrm{d}x=-\int_{-2}^{4} x^3 \mathrm{d}x=-60 (voir éxercice précédent)

Linéarité de l’intégrale

Soient f et g deux fonctions continues sur l’intervalle I. Soient a\in I et b\in I. On a:

• \int_{a}^{b} (f+g)(x) \mathrm{d}x=\int_{a}^{b} f(x) \mathrm{d}x+\int_{a}^{b} g(x) \mathrm{d}x
• \forall \lambda \in \mathbb{R}, \int_{a}^{b} (\lambda f)(x) \mathrm{d}x=\lambda \int_{a}^{b} f(x) \mathrm{d}x

Exemple

Calculer \int_{-1}^{1} 3e^x+x^2 \mathrm{d}x.

x\mapsto 3e^x, x\mapsto e^x et g:x\mapsto x^2 sont des fonctions continues sur [-1;1].
Donc \int_{-1}^{1} 3e^x+x^2 \mathrm{d}x=\int_{-1}^{1} 3e^x\mathrm{d}x+\int_{-1}^{1} x^2\mathrm{d}x=3\int_{-1}^{1} e^x\mathrm{d}x+\int_{-1}^{1} x^2\mathrm{d}x
\int_{-1}^{1} 3e^x+x^2 \mathrm{d}x=3\left[e^x\right]_{-1}^1+\left[\frac{1}{3}x^3\right]_{-1}^1=3\left(e^1-e^{-1}\right)+\frac{1}{3}\times 1^3-\frac{1}{3}\times (-1)^3
\int_{-1}^{1} 3e^x+x^2 \mathrm{d}x=3e-\frac{3}{e}+\frac{1}{3}+\frac{1}{3}=3e-\frac{3}{e}+\frac{2}{3}

Relation de Chasles

Soit f et g deux fonctions continues sur l’intervalle I.
Pour tout réels c, d, e de l’intervalle I, on a:
\int_{c}^{d} f(x)\mathrm{d}x+\int_{d}^{e} f(x) \mathrm{d}x=\int_{c}^{e} f(x) \mathrm{d}x

Propriété

Soit f une fonction continue sur l’intervalle [a;b] avec a\in \mathbb{R} et b\in \mathbb{R} tels que a < b.

• Si \forall x \in [a;b], f(x)\ge 0, alors \int_{a}^{b} f(x)\mathrm{d}x\ge 0.
• Si \forall x \in [a;b], f(x)\le 0, alors \int_{a}^{b} f(x)\mathrm{d}x\le 0.

Exemple

Démontrer que \int_{0}^{1} 1-e^x\mathrm{d}x\le 0.

Soit x\in [0;1].
x\ge 0\Leftrightarrow e^x\ge 1 \Leftrightarrow 0\ge 1-e^x \Leftrightarrow 1-e^x\le 0
Donc \forall x\in [0;1], 1-e^x\le 0.
Ainsi \int_{0}^{1} 1-e^x\mathrm{d}x\le 0.

Propriété

Soient f et g deux fonctions continues sur l’intervalle [a;b] avec a\in \mathbb{R} et b\in \mathbb{R} tels que a < b.
Si \forall x \in [a;b], f(x)\le g(x), alors \int_{a}^{b} f(x)\mathrm{d}x\le \int_{a}^{b} g(x)\mathrm{d}x.

Exemple

Soit b\in\mathbb{R}_+^*.

1. Démontrer que \forall x\in\mathbb{R}_+^*, 1-e^x-x\le 0.
2. En déduire que \int_{0}^{b} 1-e^x\mathrm{d}x \le \frac{b^2}{2}

1.Soit f la fonction définie sur \mathbb{R}_+^* par f(x)=1-e^x-x.
f est dérivable sur \mathbb{R}_+^* car x\mapsto e^x et x\mapsto 1-x le sont.
f'(x)=-e^x-1
Donc \forall x\in\mathbb{R}_+^*, f'(x)\le 0.
Ainsi la fonction f est décroissante sur \mathbb{R}_+^*.
Et donc \forall x\in\mathbb{R}_+^*, f(x)\le f(0).
C’est-à-dire \forall x\in\mathbb{R}_+^*, f(x)\le 1-e^0-0
Soit \forall x\in\mathbb{R}_+^*, f(x)\le 0
2.\forall x\in\mathbb{R}_+^*, f(x)\le 0 \Leftrightarrow \forall x\in\mathbb{R}_+^*, 1-e^x-x\le 0\Leftrightarrow \forall x\in\mathbb{R}_+^*, 1-e^x\le x
Donc \int_{0}^{b} 1-e^x\mathrm{d}x\le \int_{0}^{b} x\mathrm{d}x.
Ainsi \int_{0}^{b} 1-e^x\mathrm{d}x\le \left[\frac{1}{2}x^2\right]_0^b
\int_{0}^{b} 1-e^x\mathrm{d}x\le \frac{1}{2}b2-\frac{1}{2}\times 0^2
\int_{0}^{b} 1-e^x\mathrm{d}x \le \frac{b^2}{2}

Définition

Soit f une fonction continue sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a< b.
La valeur moyenne de la fonction f sur [a;b] est le nombre réel \mu tel que:
\mu=\frac{1}{b-a}\int_{a}^{b} f(x) \mathrm{d}x

2. Aires et intégrales

---

Propriété

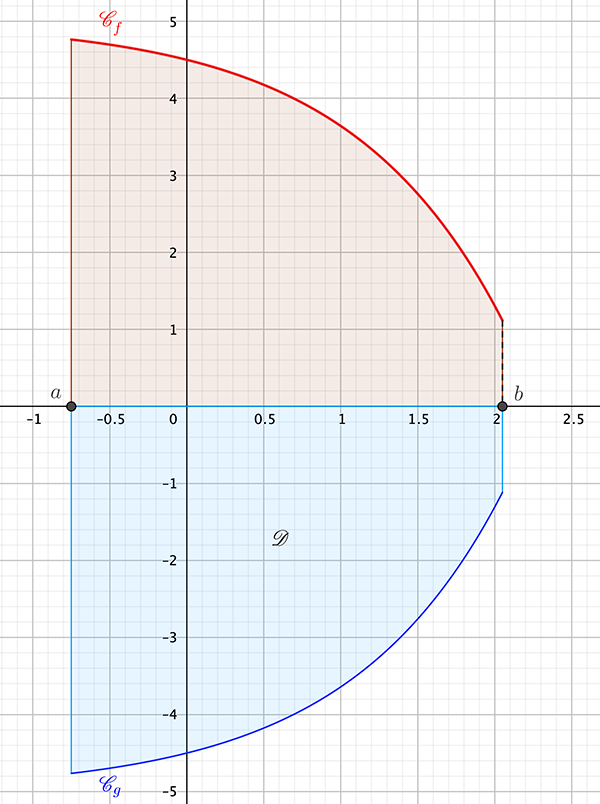
Soit g une fonction continue négative sur un intervalle [a;b], avec a\in\mathbb{R}, b\in\mathbb{R} et a< b.
Soit f la fonction définie sur [a;b] par f(x)=-g(x).
f est donc une fonction continue positive sur [a;b].

L’aire en bleue sur le graphique précédent est égale à l’aire en rouge.
Ainsi \mathscr{A}_{bleue}=\mathscr{A}_{rouge}=\int_{a}^{b} f(x) \mathrm{d}x=\int_{a}^{b} -g(x) \mathrm{d}x=-\int_{a}^{b} g(x) \mathrm{d}x.

Exemple

Déterminer l’aire \mathscr{A} comprise entre l’axe des abscisse, les droites d’équation x=1 et x=2 et la courbe \mathscr{C}_f représentative de la fonction f définie sur [1;2] par f(x)=x^2-4.

1\le x\le 2 \Leftrightarrow 1\le x^2\le 4 \Leftrightarrow -3\le x^2-4\le 0
Donc \forall x\in [1;2], f(x)\le 0
Ainsi \mathscr{A}=- \int_{1}^{2} f(x) \mathrm{d}x=- \int_{1}^{2} x^2-4 \mathrm{d}x=-\left[\frac{1}{3}x^3-4x\right]_1^2
\mathscr{A}=-\left[\left(\frac{1}{3}2^3-4\times 2\right)-\left(\frac{1}{3}1^3-4\times 1\right)\right]=-\left[\frac{8}{3}-8-\frac{1}{3}+4\right]=-\left(\frac{7}{3}-4\right)
\mathscr{A}=4-\frac{7}{3}=\frac{12}{3}-\frac{7}{3}=\frac{5}{3}

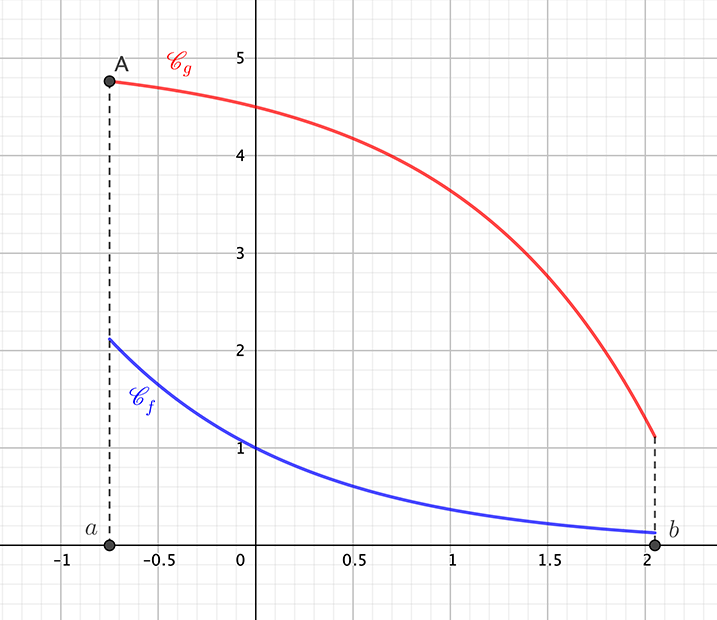
Propriété

Soient f et g deux fonctions continues sur l’intervalle [a;b] avec a\in \mathbb{R} et b\in \mathbb{R} tels que a < b.
On note \mathscr{C}_f et \mathscr{C}_g les courbes représentatives des fonctions f et g dans un repère orthogonal.
De plus, \forall x\in[a;b], f(x)\le g(x).
L’aire comprise entre les deux courbes et délimité par les droites d’équation x=a et x=b vaut:
\int_{a}^{b} g(x)-f(x) \mathrm{d}x

Exemple

Soit f et g les fonctions définies sur [-1;1] par f(x)=2x+1 et g(x)=5-\frac{1}{2}e^x. On note \mathscr{C}_f et \mathscr{C}_g les courbes représentatives des fonctions f et g dans un repère orthonormé.

1. Démontrer que \forall x\in[-1;1], f(x)\le g(x).
2. Déterminer l’aire \mathscr{A} comprise entre \mathscr{C}_f, \mathscr{C}_g et les droites d’équation x=-1 et x=1.

1.Posons \forall x\in[-1;1], h(x)=g(x)-f(x)=5-\frac{1}{2}e^x-(2x+1)=4-2x-\frac{1}{2}e^x.
h est une fonction dérivable sur [-1;1] car f et g le sont.
h'(x)=-2-\frac{1}{2}e^x
or -1\le x\le 1
donc e^{-1}\le e^x\le e^1
-e^{-1}\ge -e^x\ge -e
-2-e^{-1}\ge -4-e^x\ge -2-e
-2-e^{-1}\ge h'(x)\ge -2-e
Ainsi \forall x\in[-1;1], h'(x)\le 0
Donc la fonction h est décroissante sur [-1;1].
Et donc \forall x\in[-1;1], h(x)\ge h(1)
\forall x\in[-1;1], h(x)\ge 4-2\times 1-\frac{1}{2}e^1
\forall x\in[-1;1], h(x)\ge 2-\frac{e}{2}
\forall x\in[-1;1], h(x)\ge 0
\forall x\in[-1;1], g(x)\ge f(x)
Donc on a:
\mathscr{A}=\int_{-1}^{1} g(x)-f(x) \mathrm{d}x=\int_{-1}^{1} h(x) \mathrm{d}x=\int_{-1}^{1} 4-2x-\frac{1}{2}e^x \mathrm{d}x
\mathscr{A}=\left[4x-x^2-\frac{1}{2}e^x\right]_{-1}^1=\left(4\times 1 - 1^2-\frac{1}{2}e^1\right)-\left(4\times (-1) - (-1)^2-\frac{1}{2}e^{-1}\right)
\mathscr{A}=4-1-\frac{e}{2}+4+1+\frac{1}{2e}=8+\frac{1}{2e}-\frac{e}{2}

IV – Quelques problèmes

---

1. Quadrature de la parabole par la méthode d’Archimède

---

Dans son traité La quadrature de la parabole (lettre à son ami Dosithée), Archimède démontre un résultat particulier sur l’aire d’un segment de parabole (région délimitée par une parabole et une corde).

Nous alons conjecturer, puis de prouver cette propriété.

f est la fonction définie sur \mathbb{R} par f(x) = x^2.
Dans un repère orthonormé d’origine O, \mathscr{P} est sa courbe représentative.
A est un point mobile sur \mathscr{P}. On note a son abscisse, avec a > O.
B est le milieu du segment [OA] et C est le point de \mathscr{P}, de même abscisse que B.

Partie A: conjecturer avec un logiciel de géométrie

1. Réaliser la figure ci-dessous avec Geogebra.
   
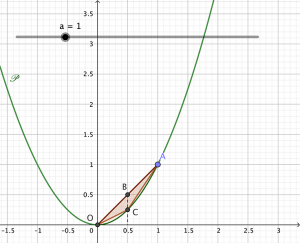
   • créer un curseur a allant de O à 5 avec pour incréament 0,1.
   • créer \mathscr{P}, A, B et C.
   • saisir IntégraleDomaine(ax, f, 0, a)[/katex] pour obtenir l'aire \mathscr{A}, en u.a., du domaine compris entre \mathscr{P} et la droite (OA) sur [O; a] (le logiciel note b cette aire).
   • créer le triangle OAC (le logiciel note t1 son aire).
   • saisir Rapport=b/t1[/katex].

   


   


2. Déplacer le curseur et conjecturer la valeur de Rapport[/katex].




Partie B: prouver la propr iété d'Archimède
D et H sont les milieux respectifs des segments [OB] et [AB], E et I sont les points de \mathscr{P} respectivement de même abscisse que D et H. L'intersection des droites (OC) et (DE) est le point G.

1. a. Exprimer les coordonnées des points B, D, C, E en fonction de a.
   On admet que G\left(\frac{a}{4};\frac{a^2}{8}\right).
   b. Vérifier que aire(OBC) = \frac{a^3}{16} et aire(OCE) = \frac{a^3}{64}.
   c. En déduire que aire(OEC) = \frac{1}{4} aire(OBC).
2. On admet que aire (ACI) = \frac{1}{4} aire(ABC). Ainsi en prenant l'aire du triangle OAC comme unité d'aire, on a donc aire(OEC) + aire(ACI) = \frac{1}{4} aire(OAC) = \frac{1}{4}.
   On réitère le procédé précédent et on obtient successivement la somme totale des aires des triangles à chaque étape (voir ci-dessous).

• 1ère étape: 1+\frac{1}{4}
• 2ème étape: 1+\frac{1}{4}+\frac{1}{16}
• ...
• n-ième étape: S_n=1+\frac{1}{4}+\frac{1}{16}+...+\frac{1}{4^n}
  a. En remarquant que \frac{1}{4^p}=\frac{1}{3\times 4^{p-1}}-\frac{1}{3\times 4^p} pour p\in\mathbb{N}^*, démontrer que S_n+\frac{1}{3\times 4^n}=\frac{4}{3}.
  b. Déterminer la limite de la suite \left(\frac{1}{3\times 4^n}\right) lorsque n tend vers en +\infty.
  c. Conclure et énoncer la propriété établie par Archimède.

2. Estimation de l'aire sous la courbe par la méthode de Monté-Carlo

---

f est la fonction définie sur l'intervalle [O; 2] par f(x) = e^{-x^2}.
\mathscr{C} est la courbe représentative de la fonction f dans un repère orthonormé \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right) et \mathscr{D} est le domaine situé sous la courbe \mathscr{C} sur [O; 2).

On note A et B les points de coordonnées respectives (2; 0) et (2; 1).

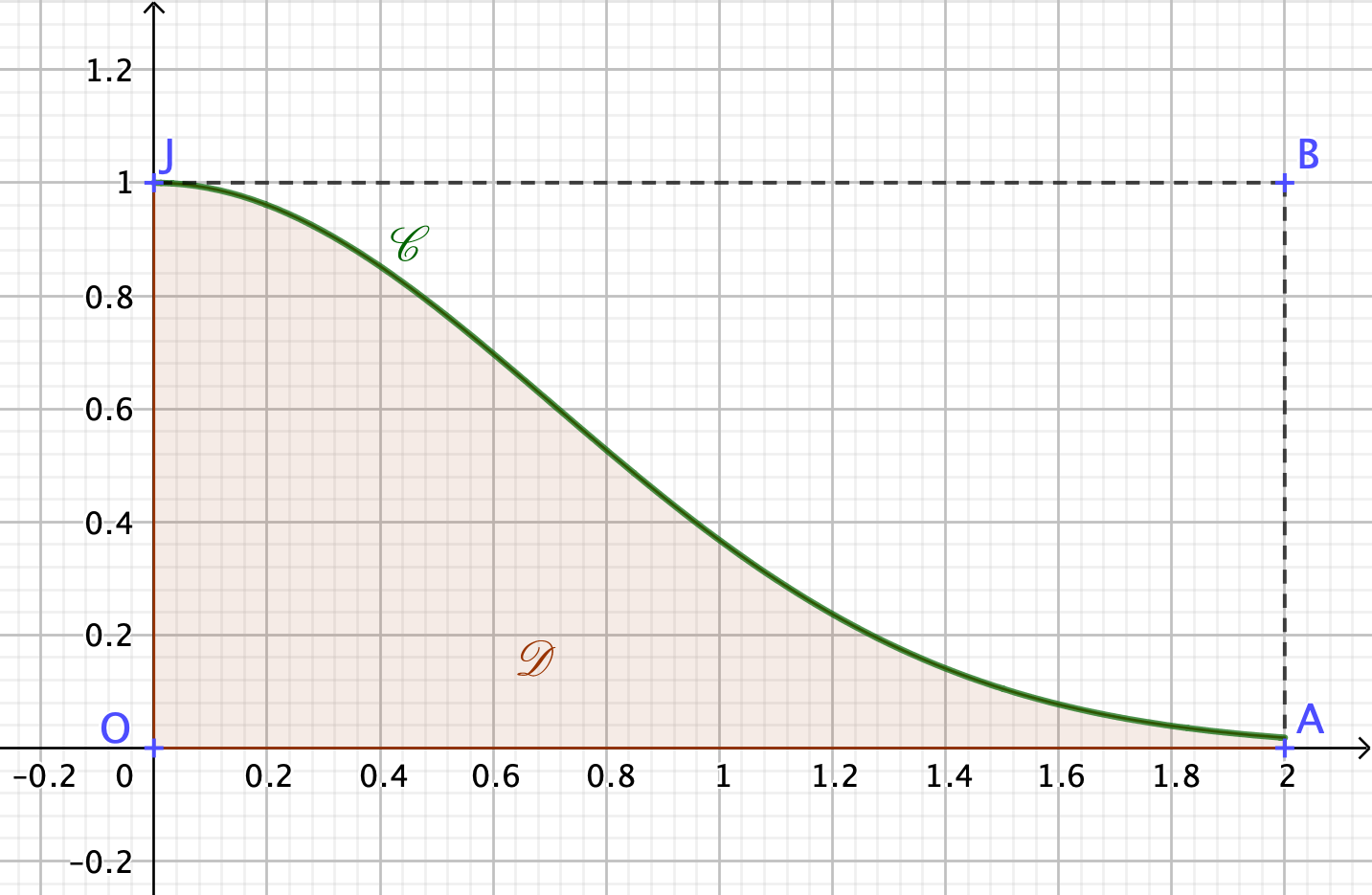
Nous allons estimer l'aire, en u.a., de \mathscr{D} à l'aide de nombres aléatoires.

1. Étudier un programme en langage Python
   Voici une fonction M_C[/katex] écrite en langage Python.

   from math import exp
   from random import random
   
   def M_C(N):
       L=0
       for k in range(1,N+1):
           x=2*random()
           y=random()
           if y<exp(-x**2):
               L=L+1
       S=2*L/N
       return S[/katex]

   Elle effectue N choix au hasard d'un point dans le rectangle OABJ et compte le nombre L de points qui sont situés dans le domaine \mathscr{D}.
Le rapport \frac{L}{N} est alors une approximation du rapport de l'aire du domaine \mathscr{D} à l'aire du rectangle OABJ.
a. Que représentent les variables x et y dans le contexte de la méthode décrite?
b. Expliquer le rôle de la condition y < e^{-x} du test à la ligne 9 du programme.
c. La fonction M_C[/katex] renvoie pour résultat le contenu de la variable S. Que représente-t-il ?

   


2. Exécuter le programme
   a. Saisir ce programme.
   b. Exécuter la fonction avec des valeurs du paramètre N de plus en plus grandes.
   Comparer les résultats à la valeur de \int_{0}^{2} e^{-x^2}\mathrm{d}x donnée par la calculatrice ci-dessous:

   \int_{0}^{2} e^{-x^2}\mathrm{d}x
   0.8820813908

3. Approximation de \pi et périmètre d'un cercle

---

Dans un repère orthonormé \left(O;\overrightarrow{OI},\overrightarrow{OJ}\right), \mathscr{C} est le cercle de centre O et de rayon 1.
On construit un triangle équilatéral de centre O inscrit dans le cercle \mathscr{C}, puis on construit de proche en proche les polygones réguliers dont le nombre de côtés est le double du précédent.

Nous allons définir deux suites qui encadrent \pi de plus en plus finement.

Partie A: Premières étapes
L'apothème a d'un polygone régulier est la distance de son centre O à chacun de ses côtés.
À l'étape i(i \in \{ 1; 2\} ), a_i désigne l'apothème du polygone régulier inscrit à l'étape i.
Pour le polygone régulier, on note b_i son demi-côté, P_i son périmètre et S_i son demi-périmètre.

1. a. Faire une figure de l'étape 1.
   b. Montrer que a_1=\frac{1}{2}, b_1=\frac{\sqrt{3}}{2}, P_1=2^1\times 3\times b_1 et S_1=\frac{3\sqrt{3}}{2}.
2. a. Faire une figure de l'étape 2.
   b. Montrer que a_2=\frac{\sqrt{3}}{2}, b_2=\frac{1}{2}, P_2=2^2\times 3\times b_2 et S_2=3.

Langage Python
On poursuit la construction précédente, on admet que l'on obtient pour tout entier naturel n\ge 1, a_{n+1}=\sqrt{\frac{1+a_n}{2}}, b_{n+1}=\sqrt{\frac{1-a_n}{2}} et S_n=\frac{2^n\times 3\times b_n}{3}.
S_n est une approximation du demi-périmètre de \mathscr{C}.

1. Voici une fonction Ar[/katex] écrite en langage Python.

   from math import sqrt
   
   def Ar(n):
       a=1/2
       b=sqrt(3)/2
       for k in range(1,n):
           b=sqrt((1-a)/2)
           a=sqrt((1+a)/2)
       S=(2**n*3*b)/2
       return S[/katex]

   Expliquer pourquoi, pour une valeur donnée du paramètre, la fonction Ar[/katex] renvoie pour résultat S_n.

   


2. Saisir et exécuter cette fonction pour les valeurs suivantes du paramètre n:
   • n=5
   • n=10
   • n=15
3. Vers quel nombre réel converge la suite \left(S_n\right)? Expliquer.
4. En utilisant un polygone régulier à 96 côtés inscrit dans le cercle \mathscr{C}, Archimède obtenait 3+\frac{10}{71} pour valeur approchée de \pi.
   Combien de décimales exactes en connaissait -il?

4. Quadrature de l'hyperbole par la méthode de Grégoire de Saint-Vincent

---

f est la fonction définie sur l'intervalle [ 1; +\infty[ par f(x)=\frac{1}{x}.
\mathscr{C} est la courbe représentative de la fonction f dans un repère orthogonal.

Nous allons mettre en évidence le comportement logarithmique de l'aire sous
l'hyperbole \mathscr{C}.

Partie A: idée de la méthode
t désigne un nombre réel strictement positif. (a_n) est la suite géométrique de raison 1 + t telle que a_1 = 1.

1. Pour tout entier n \ge 1, exprimer a_n en fonction de n.
   En déduire les valeurs de a_2, a_3, a_4 sous forme fractionnaire.
2. Grégoire de Saint-Vincent considère alors les rectangles dont les sommets ont pour coordonnées (a_i,0), (a_{i+1},0), \left(a_{i+1},\frac{1}{a_{i+1}}\right), \left(a_{i},\frac{1}{a_{i}}\right) avec i \in \mathbb{N}, i \ge 1.
   A l'étape i(i \in \mathbb{N}, i \ge 1), A_i désigne l'aire, en u.a., du nouveau rectangle construit et S_i = A_1 + A_2 + ... +A_i.
   a. À chaque étape, c'est-à-dire pour i \in \{1; 2; 3\}, exprimer A_i et S_i en fonction de t.
   Emettre une conjecture sur la nature de chacune des suites (A_i) et (S_i).
   b. n désigne un nombre entier naturel n \ge 1.

• Exprimer A_n en fonction de t.
• Exprimer S_n en fonction de n et t.
• Commenter le résultat le plus important énoncé par Grégoire de Saint-Vincent:
  « Si les abscisses d'une hyperbole équilatère croissent en progression géométrique, les aires des surfaces découpées entre l'hyperbole et son asymptote par les lignes ordonnées correspondantes croissent en progression arithmétique. »

Partie B: l'intervention des logarithmes
Grégoire de Saint-Vincent ne fait aucune allusion aux logarithmes. Or, quelques années auparavant, John Neper avait introduit la notion de logarithme en utilisant le fait qu'il transforme une suite géométrique en suite arithmétique. En 1649, Alphonse Antoine de Saressa (un lecteur admiratif de Saint-Vincent), fait le rapprochement entre logarithme et aire sous l'hyperbole.

1. Avec les notations modernes, calculer l'aire \Sigma_n, en u.a., sous la courbe \mathscr{C} sur l'intervalle [1; a] où n désigne un nombre entier supérieur à 1.
2. Lorsque n est grand et t proche de , S_n est une approximation de \Sigma_n. Expliquer alors pourquoi ln(1 + t) \approx t au voisinage de .

5. Quadrature de l'hyperbole par la méthode de Brouncker

---

f est la fonction définie sur l'intervalle [ 1; +\infty[ par f(x)=\frac{1}{x}.
\mathscr{C} est la courbe représentative de la fonction f dans un repère orthogonal.

Nous allons estimer ln(2) en utilisant l'aire sous une hyperbole.

1. Premières étapes
   À l'étape i (i \in \{1; 2 ; 3 ; 4\} ), S_i désigne la somme des aires, en u.a., des rectangles colorés sur la figure correspondante.
   
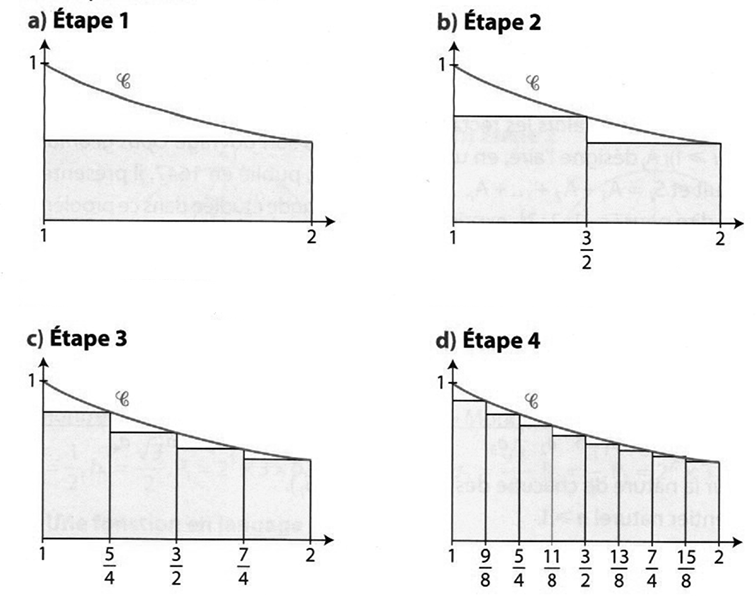
   Justifier que :
   • S_1=\frac{1}{1\times 2}
   • S_2=S_1+\frac{1}{3\times 4}
   • S_3=S_2+\frac{1}{5\times 6}+\frac{1}{7\times 8}
   • S_4=S_3+\frac{1}{9\times 10}+\frac{1}{11\times 12}+\frac{1}{13\times 14}+\frac{1}{15\times 16}
2. Une fonction en langage Python
   On poursuit la construction précédente, on admet que l'on obtient pour tout entier naturel n\ge 1, S_n=\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+...+\frac{1}{\left(2^n-1\right)\times 2^n}.
   a. Justifier que la suite (S_n) converge vers ln(2).
   b. Voici une fonction Br()[/katex] écrite en langage Python.

   def Br(n):
       S=0
       for k in range(2,2**n+1,2):
           S=S+1/((k-1)*k)
       return S[/katex]

   Expliquer pourquoi, pour une valeur donnée du paramètre n, la fonction Br()[/katex] renvoie pour résultat S_n.
c. Saisir et exécuter cette fonction pour les valeurs suivantes du paramètre:

   • n=5
   • n=10
   • n=20