Chapitre 01 – Optimisation du transport de l’électricité

I. Polynômes du second degré

définition

La fonction f est une fonction polynôme du second degré lorsqu’il existe trois nombres réels $a$ , $b$ et $c$ avec $a\neq0$ tels que $\forall x\in \mathbb{R}, f(x)=ax^2+bx+c$ .

Exemple:

Parmi les fonctions suivantes, lesquelles sont des fonctions polynômes du second degré?
$f:x\mapsto 3x^2+2x-5$
$g:x\mapsto -2x^2+3x-7$
$h:x\mapsto x(2x-3)$
$i:x\mapsto \frac{1}{x}$
$j:x\mapsto \frac{3x^2+2x-5}{2x^2-7x+1}$
$k:x\mapsto x^3+6x-1$
$l:x\mapsto x^2-3x$

Les fonctions $f$ , $g$ , $h$ et $l$ sont des fonctions polynômes du second degré.

Courbe représentative

La courbe représentative d’une fonction $P$ polynôme du second degré définie par $P(x)=ax^2+bx+c$ est une parabole d’équation $y=ax^2+bx+c$ .
Elle possède un axe de symétrie d’équation $x=\frac{-b}{2a}$ .

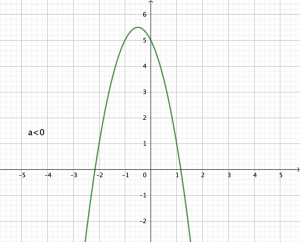
Variations et extremum de la fonction $P:x\mapsto ax^2+bx+c$

Une fonction polynôme du second degré $P:x\mapsto ax^2+bx+c$ admet un extremum:

Si $a>0$ , alors $P$ admet un minimum égal à $\beta=P(\alpha)$ et atteint pour $x=\alpha=\frac{-b}{2a}$ . De plus $P$ est décroissante sur $\left]-\infty;\alpha\right]$ et croissante sur $\left[\alpha;+\infty\right[$ .

Si $a<0$ , alors $P$ admet un maximum égal à $\beta=P(\alpha)$ et atteint pour $x=\alpha=\frac{-b}{2a}$ . De plus $P$ est croissante sur $\left]-\infty;\alpha\right]$ et décroissante sur $\left[\alpha;+\infty\right[$ .

On a donc le tableau de variation suivant:
Si $a>0$ :

$x$ $-\infty$ $\alpha$ $+\infty$

$f(x)$ $\beta$

si $a<0$ :

$x$ $-\infty$ $\alpha$ $+\infty$

$f(x)$ $\beta$
$~$

$x$	$-\infty$ $\alpha$ $+\infty$
$f(x)$	$\beta$

$x$	$-\infty$ $\alpha$ $+\infty$
$f(x)$	$\beta$ $~$

Exemple:

Déterminer l’extremum local de la fonction $P$ définie sur $\mathbb{R}$ par $P(x)=-2x^2+3x-7$ .

$P$ est une fonction polynôme du second degré.
$a<0$ , $\alpha=\frac{-3}{2\times(-2)}=\frac{3}{4}$ et $\beta=P(\alpha)=-2\alpha^2+3\alpha-7=-2\left(\frac{3}{4}\right)^2+3\times\left(\frac{3}{4}\right)-7=-2\times\frac{9}{16}+\frac{9}{4}-7=-\frac{9}{8}+\frac{18}{8}-\frac{56}{8}=-\frac{47}{8}$ .
Donc $P$ admet un maximum qui vaut $-\frac{47}{8}$ et qui est atteint pour $x=\frac{3}{4}$ .
De plus, $P$ est croissante sur $\left]-\infty;\frac{3}{4}\right]$ et décroissante sur $\left[\frac{3}{4};+\infty\right[$ .
On a donc le tableau de variations suivant:

$x$ $-\infty$ $\frac{3}{4}$ `$$+\infty$$

$f(x)$ $-\frac{47}{8}$
$~$

$x$	$-\infty$ $\frac{3}{4}$ `$$+\infty$$
$f(x)$	$-\frac{47}{8}$ $~$

II. Les graphes orientés

Définition et vocabulaire
Définition
Un graphe orienté est composé:

de sommets
des arcs reliant des couples de sommets dans un sens donné, représentés par des flèches.

Exemple de graphe
Voici la représetnation d’un graphe.

Il possède 4 sommets d’étiquettes a, b, c, d.
Il possède aussi 5 arcs:

de a vers b
de a vers c
de d vers a
de c vers d
de b vers c

Vocabulaire

L’origine de l’arc est le sommet duquel part l’arc. On l’appelle aussi source de l’arc.

Le but de l’arc est le sommet vers lequel pointe l’arc.

Un successeur d’un sommet $x$ est un sommet but d’un arc d’origine $x$ .

Un prédécesseur d’un sommet $y$ est un sommet origine d’un arc de but $y$ .

Exemple
Avec le graphe orienté précédent, on peut remplir le tableau ci-dessous:

Sommet	prédécesseurs	successeurs
a	d	b , c
b	a	c
c	a , b	d
d	c	a

Modélisation d’un réseau électrique
On peut modéliser un réseau électrique par un graphe:

les sources électriques, les cibles et les noeuds intermédiaires sont des sommets.
les lignes hautes, moyennes et basses tensions sont les arcs ayant des poids égaux à l’effet Joule.

Le but est de minimiser les pertes dues à l’effet Joule.

Dans un réseau électrique construit de façon optimale, on a les contraintes suivantes:

La somme des intensités entrantes dans un noeud intermédiaire est égale à la somme des intensités sortantes.
L’intensité totale arrivant à chaque cible est imposée par l’intensité utilisée par la cible.
Les sources peuvent fournir au maximum les puissances $P_{max}$ .

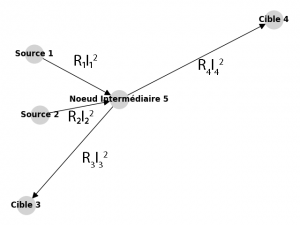
Comme l’intensité totale arrivant aux cibles est fixée, les pertes par effet Joule ne peuvent pas être minimisées.
La perte totale des sources par effet Joule est égale à $Perte=R_1I_1^2+R_2I_2^2$ .
On peut minimiser cette perte puisque $I_1$ et $I_2$ peuvent être ajustées.
La somme des intensité entrantes est égale à la somme des intensités sortantes du noeud intermédiaire donc: $I_1+I_2=I_3+I_4$ .

Il vient donc que $I_2=I_3+I_4-I_1$ .
Ainsi $Perte=R_1I_1^2+R_2(I_3+I_4-I_1)^2$ .
En développant cette dernière expression, on obtient un polynôme du second degré en $I_1$ .
Il suffit alors de trouver le minimum de cette fonction $Perte$ .

Exemple:

Dans le réseau de distribution précédent:

la source 1 délivre une puissance maximale de 18000W avec une tension de 360V et une résistance de 0,6 $\Omega$ .
la source 2 délivre une puissance maximale de 9000W avec une tension de 260V et une résistance de 0,8 $\Omega$ .
la cible 3 délivre une puissance de 3kW avec une tension de 230V.
la cible 4 délivre une puissance de 15kW avec une tension de 230V.

Déterminer les pertes par effet Joule minimales.

On a donc $R_1=0,6$ , $R_2=0,8$ , $I_{1_{max}}=\frac{18000}{360}=50$ , $I_{2_{max}}=\frac{9000}{260}\approx 34,6$ , $I_3=\frac{3000}{230}\approx 13,0$ et $I_4=\frac{15000}{230}\approx 65,2$ .

Ainsi on obtient $Perte=0,6\times I_1^2+0,8(13,0+65,2-I_1)^2=0,6\times I_1^2+0,8(78,2-I_1)^2$

$Perte=0,6\times I_1^2+0,8(78,2^2-2\times 78,2\times I_1+I_1^2)=0,6\times I_1^2+4892,192-125,12I_1+0,8I_1^2$
$Perte=1,4I_1^2-125,12I_1+4892,192$

La perte minimale devrait donc être atteinte pour $I_1=\frac{-(-125,12)}{2\times 1,4}\approx 44,69A$ .
On a bien $44,69\le 50$ , c’est-à-dire $I_1\le I_{1_{max}}$ .
Donc la perte minimale est atteinte pour $I_1=44,69A$ .
Ainsi $I_2=13,0+65,2-44,69=33,51A$ , et $33,51\le 34,6$ donc $I_2=33,51A$ .

On aura donc $P_1=0,6\times 44,69^2=1198,32W\approx 1200W$ et $P_2=0,8\times 33,51^2=898,34W\approx 900W$ .