I. Les suites géométriques
Définition
Soit q un nombre réel fixé. On dit que
$$v [/katex]$$est une suite géométrique de raison$$q [/katex]$$si et seulement si on obtient chaque terme de cette suite en multipliant le terme précédent par q.
On a donc \forall n \in \mathbb{N}, v(n+1)=q \times v(n).
Remarque
On ne s'intéressera qu'aux suites géométriques à raison strictement positive ( q>0).
Propriété
Soit
$$v [/katex]$$une suite géométrique de raison q.
\forall n \in \mathbb{N}, \forall p \in \mathbb{N}, v(n)=v(p) \times q^{n-p}
En particulier \forall n \in \mathbb{N}, v(n)=v(0) \times q^n
Représentation graphique
Pour la représentation graphique d'une suite géométrique
$$v [/katex]$$de raison q, on parle d'évolution exponentielle.
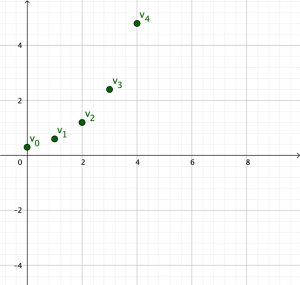
Cas où v(0)>0 et q>1
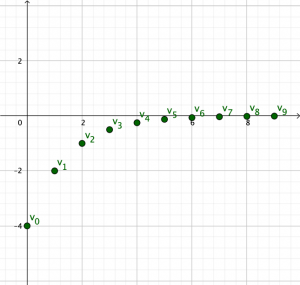
Cas où v(0)>0 et 0 < q < 1
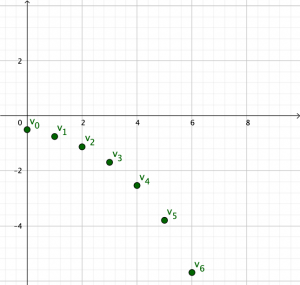
Cas où v(0)<0 et q>1
Cas où v(0)<0 et 0 < q < 1
Propriété
Soit v une suite géométrique de raison q.
- Si q>1 et v(0)>0 alors \lim\limits_{n \rightarrow +\infty} v(n)=+\infty
- Si q>1 et v(0)<0 alors \lim\limits_{n \rightarrow +\infty} v(n)=-\infty
- Si 0 < q < 1 alors \lim\limits_{n \rightarrow +\infty} v(n)=0
- si q=1 alors \lim\limits_{n \rightarrow +\infty} v(n)=v(0)
Propriété 5
Une grandeur discrète v varie de façon exponentielle en fonction du palier entier nsi sa variation absolue u(n+1)-u(n) est proportionnelle à sa valeur courante u(n). Dans ce cas, son taux de variation est constant et la suite de terme général u(n) est géométrique.
Exemple de modèle exponentiel avec les suites géométriques
A un instant t=0, une population de bactéries compte 20000 bactéries. Chaque heure, la population augmente de 10%.
On pose v(n) le nombre de bactéries (en milliers) de cette population lors de l'instant n, avec n\in\mathbb{N}.
Si besoin, les résultats seront arrondis au millième.
- Déterminer v(0).
- Calculer v(1) et v(2).
- Exprimer v(n+1) en fonction de v(n).
- Justifier que la suite v est géométrique.
- Exprimer v(n) en fonction de n.
- Quelle sera le nombre de bactéries au bout de 5 heures ?
- Estimer au bout de combien d'heures le nombre de bactéries aura doublé?
1.v(0)=20
2.v(1)=20\times \left(1+\frac{10}{100}\right)=20\times 1,1=22
v(2)=22\times 1,1=24,2
3.v(n+1)=v(n)\times \left(1+\frac{10}{100}\right)=1,1v(n).
4.v(n+1)-v(n)=1,1v(n)-v(n)=0,1v(n).
Donc v(n+1)-v(n) est proportionnel à v(n).Ainsi v est une suite géométrique de raison 1,1 et de terme initial v(0)=20.
5.Ainsi on a v(n)=v(0)\times 1,1^n=20\times 1,1^n.
6.En 2025, n=5. v(5)=20\times 1,1^5\approx 32,210. Au bout de 5 heures, il y aura 32210 bactéries.
7.On cherche n pour que v(n)\ge40.
v(n)\ge40 \Leftrightarrow 20\times 1,1^n\ge 40 \Leftrightarrow 1,1^n\ge \frac{40}{20} \Leftrightarrow 1,1^n\ge 2
Grâce à la calculatrice, on obtient n\ge 8. Il faudra donc 8 heures pour que la population de bactéries soit doublée.
Exemple 2
Une population possède 70000000 habitants en 2020. Chaque année, son taux de natalité est de 13‰ et son taux de mortalité est de 10‰.
- Déterminer le taux d'accroissement de cette population.
- On pose u(n) le nombre d'habitants dans cette population lors de l'année 2020+n.Dans ces question, si besoins, vous arrondirez les résultats à l'unité.
a. Calculer u(1) et u(2).
b. Démontrer que la suite u est géométrique.
c. Exprimer u(n) en fonction de n.
d. Calculer le nombre d'habitants dans cette population en 2028.
e. En quelle année la population dépassera 80 millions d'habitants?
1.Le taux d'accroissement est la différence entre le taux de natalité et le taux de mortalité: 13‰-10‰=3‰.
2.a. u(1)=u(0)\times (1+\frac{3}{1000}=70000000\times 1,003=70210000
u(2)=u(1)\times 1,003=70210000\times 1,003=70420630
b.u(n+1)=u(n)\times 1,003 \Leftrightarrow \frac{u(n+1)}{u(n)}=1,003 donc \frac{u(n+1)}{u(n)} ne dépend pas de n. Ainsi la suite u est géométrique de raison 1,003 et de terme initial u(0)=70000000.
c.u étant géométrique de raison 1,003 et de terme initial u(0)=70000000, on a:
u(n)=u(0)\times 1,003^n=70000000\times 1,003^n
d.En 2028, n=8. Donc on calcule u(8):
u(8)=70000000\times 1,003^8\approx 71697746
e.u(n)\ge80000000 \Leftrightarrow 70000000\times 1,003^n\ge 80000000 \Leftrightarrow 1,003^n\ge \frac{80000000}{70000000} \Leftrightarrow 1,003^n\ge \frac{8}{7}
La calculatrice donne n\ge 45. Donc à partir de 2065 la population dépassera 80 millions d'habitants.
II. Modèle de Malthus
Thomas Robert malthus (1766-1834) était un économiste britannique. Il a prédit que, sans frein, la population anglaise augmente de façon exponentielle tandis que les ressources ne croissent que de façon arithmétique.
Propriété
Le modèle démographique de Malthus est un modèle exponentiel d'évolution de l'effectif de la population. Il prévoit que :
- si le taux de natalité est supérieur au taux de mortalité alors la population croît vers l'infini.
- si le taux de mortalité est supérieur au taux de natalité alors la population croît vers .
Ce modèle est valide sur des temps courts mais irréaliste sur des temps longs en raison de l'insuffisance des ressources.
Exercice
En 1800, l'Angleterre comptait 8 millions d'habitants.
Malthus avait émis les hypothèses suivantes:
- La population d'Angleterre suivait un progression géométrique en augmentant de 2% par an.
- l'agriculture anglaise, en 1800, permettait de nourrir 10 millions d'habitants et son amélioration permettrait de nourrir 400000 habitants supplémentaires par an, suivannt une progression arithmétique.
- Soit v(n) la population d'Angleterre (en millions d'habitants) en l'année 1800+n.Soit u(n) le nombre de personnes (en millions) que pouvait nourrir l'agriculture anglaise en l'année 1800+n.
a. Exprimer v(n) en fonction de n.
b. Exprimer u(n) en fonction de n.
c. Calculer la population d'Angleterre en 1900 et le nombre de personnes que pouvait nourrir l'agriculture anglaise en 1900. - A l'aide de la calculatrice ou d'un tableur, déterminer l'année à partir de laquelle, selon Malthus, l'agriculture anglaise ne permettrait plus de nourrir toute la population anglaise.
- Le modèle de Malthus est-il réaliste?
1.a. v est géométrique de raison 1+\frac{2}{100}=1,02 et de terme initial v(0)=8 donc v(n)=8\times 1,02^n.
b. u est une suite arithmétique de raison 0,4 et de terme initial u(0)=10 donc u(n)=10+0,4n.
c. en 1900, n=100.
v(100)=8\times 1,02^100=57,957
u(100)=10+0,4\times 100=50
En 1900, la population d'Angleterre était de 57,957 millions d'habitants et l'agriculture anglaise pouvait nourrir 50 millions d'habitants.
2.On trouve n=87, soit : en 1887, l'agriculture anglaise ne permettait plus de nourrir toute la population anglaise.
3.Le modèle de malthus n'est pas réaliste sur des périodes longues car les taux de mortalité et de natalité seraient à recalculer chaque année à partir de 1887.