I – Histoire de l’informatique
Vers 1930, Gödel invente pour faire des démonstrations d’indécidabilité un codage numérique des expressions logiques. Ce travail fournira plus tard des bases théoriques au codage informatique. Dans les codes informatiques ASCII (7 bits), ISO (8 bits), Unicode (16 bits), tous les caractères ont un équivalent numérique qui permet de passer d’une représentation interne sous forme de 0 et de 1 sur laquelle l’ordinateur calcule, à leur présentation lisible par l’homme sur un écran ou une feuille de papier.
En 1936 la machine de Turing définit abstraitement la notion de calcul et permet de définir ce qui est calculable ou non. C’est une machine abstraite qui définit les calculs comme des opérations qu’on peut enchaîner mécaniquement sans réflexion. Le « lambda-calcul » d’Alonzo Church en est l’équivalent.
Les premiers ordinateurs datent de 1950. C’est la notion de programme enregistré, due à John von Neumann et à ses collaborateurs, en 1945, qui transforme les machines à calculer en ordinateurs.

La mémoire centrale des machines est volatile et ne conserve les données que pendant la durée d’exécution des programmes. Or les fichiers doivent être conservés d’une exécution à l’autre. D’abord sous forme de paquets de cartes perforées, les fichiers sont conservés ensuite dans des mémoires auxiliaires comme des bandes magnétiques ou des disques durs (1956). Ces fichiers sont soit des programmes, soit des données.
Jusqu’aux années 1970, les ordinateurs recevaient les programmes et les données sur des cartes, des Architectures matérielles et systèmes d’exploitation rubans perforés ou des bandes magnétiques. Ils renvoyaient leurs résultats quand ils étaient terminés ou retournaient des messages d’erreur énigmatiques.
Dans les années 1970 sont apparus de nouveaux types de machines informatiques avec disque dur, écran et clavier. Elles ont d’abord fonctionné en mode « ligne de commande », purement textuel et asynchrone. Elles ont pu employer les premiers langages interprétés comme Lisp et BASIC, élaborés une décennie plus tôt. Au lieu d’écrire un programme, l’utilisateur tape une commande qui est exécutée. Il garde le contrôle du processus de calcul et peut tenir compte des résultats précédents pour enchaîner. Puis l’écran est devenu graphique et la souris a permis la manipulation directe. Les machines deviennent interactives. Le développement des interfaces ou IHM (interface homme-machine) introduit les notions d’action et d’événement dans la programmation. De ce fait, le temps compte et il n’est pas possible de recommencer une exécution à l’identique. Pour construire des interfaces facilitant l’interaction, de nouveaux concepts sont apparus comme les fenêtres, les menus déroulants, les boutons à cliquer, les cases à cocher, les formulaires. La métaphore du bureau a fait le succès du Macintosh d’Apple : elle transfère les objets (dossiers, fichiers, corbeille) et les actions du travail de secrétariat (couper, coller) dans l’univers de
l’interface.
Les premiers systèmes d’exploitation datent des années 1950, mais leur emploi s’est généralisé vers 1965. Avec la deuxième génération d’ordinateurs, la gestion des périphériques s’est alourdie. Il devint impossible pour un programmeur de concevoir à la fois les logiciels d’application et les logiciels de gestion de la machine. Une distinction s’établit donc entre les applications (programmes de l’utilisateur) et les programmes système (logiciel de gestion des ressources de la machine).

II – Les données
1. Types de fichiers
Il existe différents types de fichiers. On les reconnait grâce à leur extension (les lettres après le dernier .[/katex])
Les fichiers images:
- bitmap: extension
.bmp[/katex] - Joint Photographic Experts Group: extension
.jpg[/katex] ou.jpeg[/katex] - Portable Network Graphics: extension
.png[/katex] - Graphics Interchange Format: extension
.gif[/katex] - Tagged Image File Format: extension
.tiff[/katex] ou.tif[/katex]
Les fichiers audios:
- Waveform Audio File Format: extension
.wav[/katex] (windows principalement) - MPEG-1/2 Audio Layer III: extension
.mp3[/katex] (toutes plateformes) - Audio Interchange File Format: extension
.aiff[/katex] (apple principalement) - fichier audio au format Ogg: extension:
.oga[/katex] (format ouvert)
Les fichiers vidéos:
- Audio Video Interleave: extension
.avi[/katex] - Windows Media Video: extension
.wmv[/katex] - QuickTime: extension
.mov[/katex] - Matroska: extension
.mkv[/katex] - Flash Video: extension
.flv[/katex]
Pour les fichiers audios et vidéos, les extensions permettent de savoir de quel type de fichier il s'agit mais en aucun cas de savoir comment le fichier est compressé, ni de savoir quel codec (programme qui permet de coder et décoder un flux) est utilisé.
Les fichiers éxecutables:
- sous windows:
- extension
.exe[/katex] - extension
.com[/katex] - extension
.bat[/katex] (script executable)
- extension
- sous mac:
- pratiquement tous les fichiers peuvent être exécuté
- les extensions permettent de savoir comment le fichier sera exécuté
- extension
.app[/katex] le plus courant pour lancer une application
- sous unix:
- pratiquement tous les fichiers peuvent être exécuté
- les extensions permettent de savoir comment le fichier sera exécuté
2. Taille d'un fichier son
Une onde acoustique est un signal continu s en fonction du temps t. Il est donc représenté par la fonction t\mapsto s(t).
Numériser un tel signal, c’est passer du domaine physique (données analogiques) au domaine numérique (binaire).
Pour cela, il faut, pour chaque canal (1 en mono, 2 en stéréo, 6 en 5.1, etc.) :
- Echantillonner, c’est-à-dire, à intervalles de temps réguliers t_1 < t_2 < ⋯ < t_N, prendre les valeurs du signal s_i=s(t_i)\in\mathbb{R}.
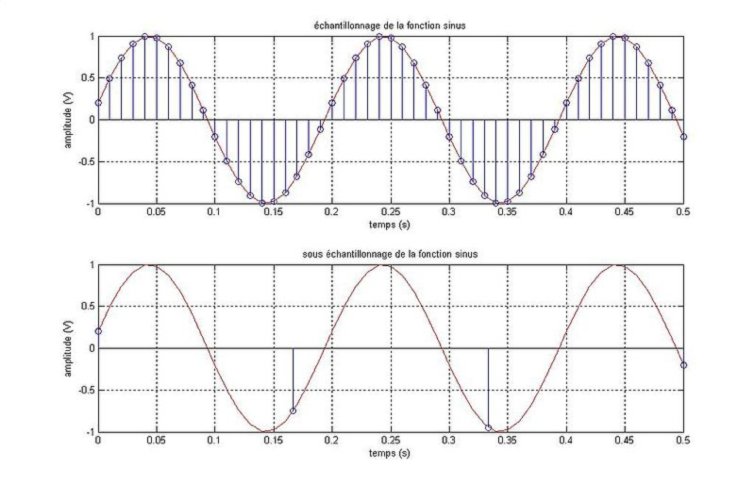
- Quantifier le signal, c’est-à-dire coder les valeurs s_i sur B bits.
Ainsi, pour calculer la taille d'un son non compressé de durée d ayant N canaux, un taux d'échantillonnage de t Hz et une quantification sur B bits, on utilise la formule suivante:
N\times d\times t\times B pour avoir sa taille en bits
\frac{N\times d\times t\times B}{8} pour avoir sa taille en octets
Exemple:
La version longue de la 9ème symphonie de Beethoven dure 74 minutes. On la numérise en stéréo avec un taux d'échantillonnage de 44,1 kHz et une quantification de 16 bits.
Déterminer la taille du fichier son non compressé en Mio (mébioctets).
1 Mio=1024 kio et 1 kio=1024 o
44,1kHz=44100Hz
74 min= 74\times 60=4440 s
Le son est enregistré en stéréo donc sur 2 canaux.
On a ainsi:
\frac{2\times 4440\times 44100\times 16}{8}=783216000octets soit \frac{783216000}{1024\times 1024}\approx 747 Mio
3. Taille d'un fichier image
Une image numérique a les caractéristiques suivantes:
- des dimensions: hauteur et largeur en pixels.
- un nombre de couches: 3 ou 4 en général.
- une profondeur en bits: 8, 16 ou 32 bits par couche
Pour calculer la taille d'une image de hauteur h et de largeur l, de profondeur B ayant N couches, on a la formule suivante:
h\times l\times N\times B pour avoir sa taille en bits
\frac{h\times l\times N\times B}{8} pour avoir sa taille en octets
Exemple:
Une photo prise par le Nikon D90 a des dimensions de 4288 pixels en largeur et 2848 pixels en hauteur. Elle est encodée sur 3 couches en 8 bits par couches.
a. Quelle est sa taille en octets, puis en Mio?
b. Une image .jpg[/katex] de même caractéristiques a une taille de 8,7 Mio. Expliquez pourquoi.
a. \frac{4288\times 2848\times 3\times 8}{8}=36636672~octets soit \frac{36636672}{1024\times 1024}\approx 35 Mio
b. Le jpeg est un format d'image compressé.
4. Taille d'un fichier vidéo
C'est identique à l'image mais on ajoute la durée. En france, à la télévision, le flux d'image est cadencé à 25 images par secondes et au cinéma à 24 images par seconde.
De plus, si le film est sonore, il faut ajouter le flux sonore.
Exemple:
Un film muet de 2h est enregistré en format numérique pour la télévision. Sa résolution est de 1920 pixels sur 1080 (qualité full HD), encodé sur 3 couches en 8 bits par couches.
a. Quelle est la taille du fichier correspondant au film en Gio?
b. Un blu-ray a une capacité de 50 Gio. Que peut-on dire des films inscrits sur les blu-ray?
a. durée: 2\times 3600=7200~s
Nombre d'images: 7200\times 25=180000~images
taille d'une image: \frac{1920\times 1080\times 3\times 8}{8}=6220800~octets
taille du fichier: 6220800\times 180000=1119744000000~octets= \frac{1119744000000}{1024\times 1024\times 1024}\approx 1042~Gio
b. Le fichier sur les blu-ray est donc compressé.
5. Taille d'une page de texte
Pour coder un caractère en binaire, on utilise un jeu de caractères codés qui associe des caractères d’un ou plusieurs systèmes d’écriture avec une représentation numérique.
Exemples de jeu de caractères : ASCII (American Standard Code for Information Interchange), ISO 8859-1, ISO-8859-1, Unicode, UTF-8…
Nous nous interesserons au codage ASCII car 1 caractère est codé sur 1 octet.
Il est donc facile de connaître la taille d'un fichier de texte connaissant son nombre de caractères.
Exemple:
Estimer la taille d'un fichier texte codé en ASCII comprenant uniquement la phrase:
L'enseignement scientifique, c'est magique!
Cette phrase comporte 43 carcatères donc sa taille devrait être de 43 octets.
III - Débogage et programmation
Un programme informatique peut contenir des milliers de lignes d'instructions. Il est naturel que parmis ces lignes, des bogues (ou bugs) soient présents.
Déboguer un programme, c'est supprimer ces bugs.
Pour cela, la plupart des logiciels de programmation possède un programme d'aide au débogage.
IV - Application de l'intelligence artificielle
L'intelligence artificielle est l'ensemble des théories et des techniques développant des programmes informatiques complexes capables de simuler certains traits de l'intelligence humaine (raisonnement, apprentissage…).
Elle consiste en 2 étapes:
- l'apprentissage machine (machine learning)
- Prise de décision
- L'apprentissage machineL'apprentissage consiste en la récupération de données. L'être humain lui fournit des données. Par exemple une IA qui fait des parties d'échec aura absorbé plusieurs dizaines de milliers de parties d'échec.
Les données absorbées sont si énormes qu'on appelle cela le big data.
- Prise de décisionL'IA peut prendre une décision en faisant une étude statistique sur les données ingérées.
Dans notre exemple de la partie d'échec, le joueur humain fait un coup et l'IA va chercher dans toutes les données accessibles les mêmes coups joués (ou les coups semblables) et choisira par étude statistique quel coup elle devra jouer.L'étude statistique utilisée est une étude de prédiction comme nous l'avons vu avec les modèles linéaires et exponentiels. Elle utilise les courbes de régression.
Toujours dans notre exemple du jeu d'echec, l'étude statistique peut porter sur le nombre de coups restant et donc utilisera une courbe de régression permettant de prévoir un nombre de coup minimum.
- Quelques exemple d'IA
- jeux d'échec, de go, autres jeux
- google, amazon, etc
- Alexa, Siri, assistant google
- voitures autonomes, trains autonomes, etc.
- gestion du traffic aérien, routier, etc.: optimisation du carburant pour un trajet, itinéraires alternatifs
- prévention médical, aide au dignostic, prédiction de maladie, chirurgie assistée par ordinateur, etc.
- problèmes éthiques
L'IA permet des progrès dans de nombreux domaines. Cependant, elle pose de nombreuses questions d'éthique:
- Si une machine peut prendre une décision, peut-elle être tenue responsable des conséquences d'une telle décision. (est-ce la machine ou le programmeur de la machine?)
- Une machine peut-elle avoir une influence sur la vie des humains sans avoir de morale? (certaines personnes n'en ont pas: licenciement, etc.)
- Quelles sont les implications de la collecte systématique de données sur tous les utilisateurs? (L'IA est là pour aider les utilisateurs et donc doit les connaître, problème de liberté et de vie privée)
V - Inférence bayésienne
L'inférence bayésienne permet de calculer la probabilité d'une cause à partir de l'observation d'événements connus.
Elle est donc utilisée en médecine: c'est le principe du diagnostic. On peut estimer la probabilité d'une maladie à partir d'un test basé sur un effet de la maladie.
La mise en place de tests correspond à un processus d'IA puisqu'elle s'appuie sur le traitement de nombreuses données.
Cependant, pour chaque test, il existe des faux positifs et des faux négatifs. Ainsi l'estimation de la probabilité de la maladie est effectuée à partir d'un test imparfait.
On doit alors faire un tableau de contingence en fonction des résultats du test et du diagnostic.
| Diagnostic | |||
| carcatère présent | caractère non présent | ||
| Résultat du test | Positif | Vrai positif | Faux positif |
| Négatif | Faux négatif | Vrai négatif | |
On appelle sensibilité la probabilité que le test soit positif sachant que le caractère est présent.
On appelle spécificité la probabilité que le test soit négatif sachant que le caractère est non présent.
Exemple:
Une IA est entraînée à reconnaître les cas de cancer du sein à partir d'une base de données publique de 1000 personnes testées.
Sur les 1000 personnes testées:
- 150 sont malades
- parmis les personnes malades, 120 ont eu un test positif.
- parmis ceux qui ont eu un test négatif, 800 ont ne sont pas atteints.
a. Etablir un tableau de contingence correspondant au test et au diagnostic.
b. Déterminer la sensibilité et la spécificité du test.
c. Une personne passe ce test et a un résultat positif. Quelle est la probabilité qu'elle soit atteinte du cancer du sein?
a.
Diagnostic atteint non atteint Total Résultat du test Positif 120 50 170 Négatif 30 800 830 Total 150 850 1000 b. sensibilité=\frac{120}{150}=0,8
spécificité=\frac{800}{850}=\frac{16}{17}\approx 0,94
c. \frac{50}{170}=\frac{5}{17}\approx 0,29
La probabilité que cette personne soit saine est de 29% environ.